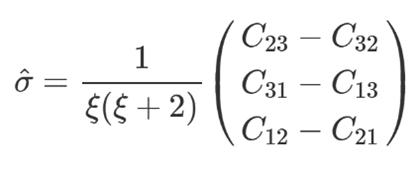欧拉角
欧拉角(Euler angle)指的是绕参考坐标系主轴(X,Y,Z)之一旋转的角度。利用最多三次欧拉角旋转,原坐标系可变换为任何新坐标系。这三个欧拉角即构成了欧拉角序列。共有12种欧拉角序列。
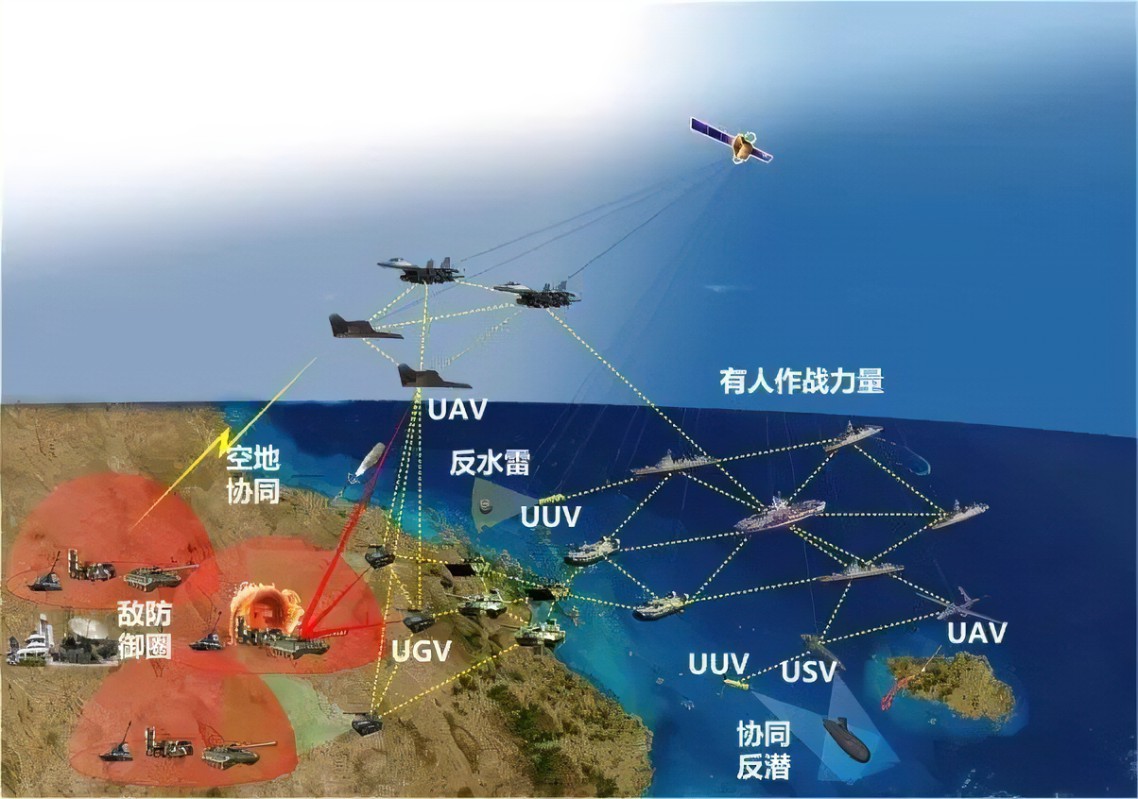
无人机的欧拉角定义在机体系下,机体轴坐标系的原点固连于飞行器重心,X轴指向机头,Z轴指向机腹,X轴和Z轴都位于纵向对称面内,Y轴指向机身右侧,与X、Z轴构成右手系。其中重要的一组欧拉角:绕Z轴转ψ为偏航角,绕Y轴转θ为俯仰角,绕X轴转φ为滚转角。
旋转矩阵
分别表示绕Z轴转ψ,绕Y轴转θ,绕X轴转φ
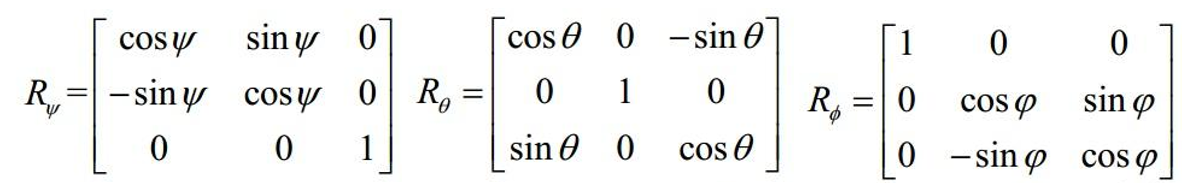
欧拉角的局限性
只要θ≠±90°,欧拉角可以描述清楚任何刚体的姿态以及角运动信息,θ=±90°出现万向锁现象。而对于大部分飞行器来说,俯仰角不会到90°,所以,使用欧拉角进行姿态控制完全可以满足使用要求,但对于一些要求高机动能力的飞行器来说,为了防止俯仰角90°时出现奇点,使用四元数替代欧拉角进行姿态控制。另外,对于姿态解算时欧拉角描述方法也会出现问题,所以使用四元数进行姿态解算。
万向锁问题出现在当两个旋转轴接近平行时,一个旋转轴的旋转会导致另外两个轴的旋转受限,从而丧失了一个旋转自由度。这种情况下,无法唯一地确定物体的姿态,因为存在多个欧拉角组合可以表示相同的旋转。
四元数
四元数是由1个实数加上3个复数组合而成,通常可以表示成q=q0+q1i+q2j+q3k或者q=(q0,q1,q2,q3),其中q0,q1,q2,q3都是实数,而i,j,k为虚数单位。
假设存在一根旋转轴u,绕u轴旋转σ角度,代表这个旋转的四元数为q=(cos(σ/2),usin(σ/2)),其中u是旋转轴的单位向量,q是一个单位四元数。
它对任何向量施加以下算子运算后可以得到该向量绕u轴旋转σ角度后的向量: w=qvq*
四元数转旋转矩阵
已知四元数: q=(q0,q1,q2,q3)
旋转矩阵为:
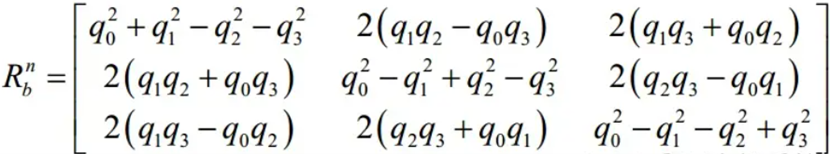
旋转矩阵转四元数
已知旋转矩阵:
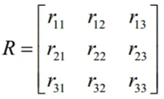
则求解四元数时根据的方法就是从四元数转旋转矩阵的公式中得到:
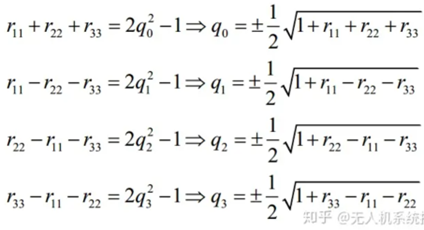
但从上式中是无法确定正负号的,所以又有:
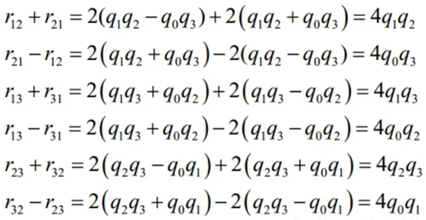
这样只要得到q0到q4中的任意一个就能根据上面的关系求出剩余3个分量的值,假设我们先求q0的值,则有:

从上式中可以看到,求得的四元数有两个,但他们表示的是同一种旋转关系,至于先求q0到q4中的哪个值,在实际使用时应该全部一起求,看哪个值大,就选取哪个,以防止某一项在出现0时无法计算的情况。
欧拉角转四元数
已知欧拉角:α、β、γ
四元数为:
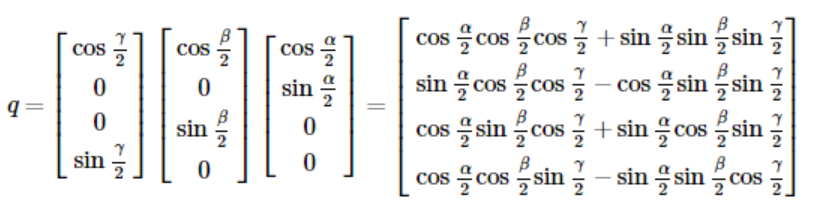
四元数转欧拉角
已知四元数: q=(q0,q1,q2,q3)
欧拉角为:
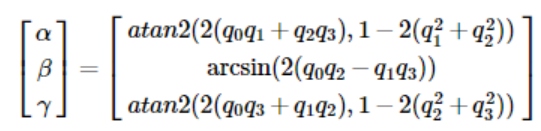
但是当β角度为90度时,四元数反向计算欧拉角时会出现奇点,无法计算。因为这时候简化后的四元数是这样的:

所以atan2中后面那一项即横坐标就变成了0: 1-2(q2^2+q3^2)=0
此时通常令α=0,然后解出欧拉角的值。
修正罗德里格斯参数
modified Rodrigues parameters又称为MRP。它是描述两坐标系之间方向关系的一种方法,且由欧拉四元数 衍生定义:
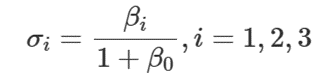
三个参数组成的向量即为修正罗德里格斯参数σ: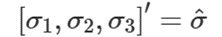
设主旋转矢量中主轴为e ,主角度为φ ,
则修正罗德里格斯参数可由两者导出: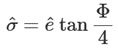
与欧拉四元数的关系
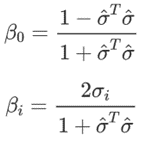
求得四元数 (β0,β1,β2,β3)
与方向余弦矩阵的关系
方向余弦矩阵用修正罗德里格斯参数表示为:
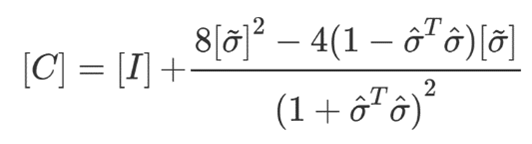
在已知方向余弦矩阵的情况下求修正罗德里格斯参数:
定义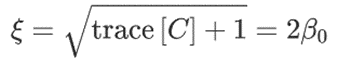
其中, β0为第一个欧拉四元数参数,trace[C]为矩阵[C]的迹。
则修正罗德里格斯参数表示为