关于脉冲压缩技术的参数变化研究

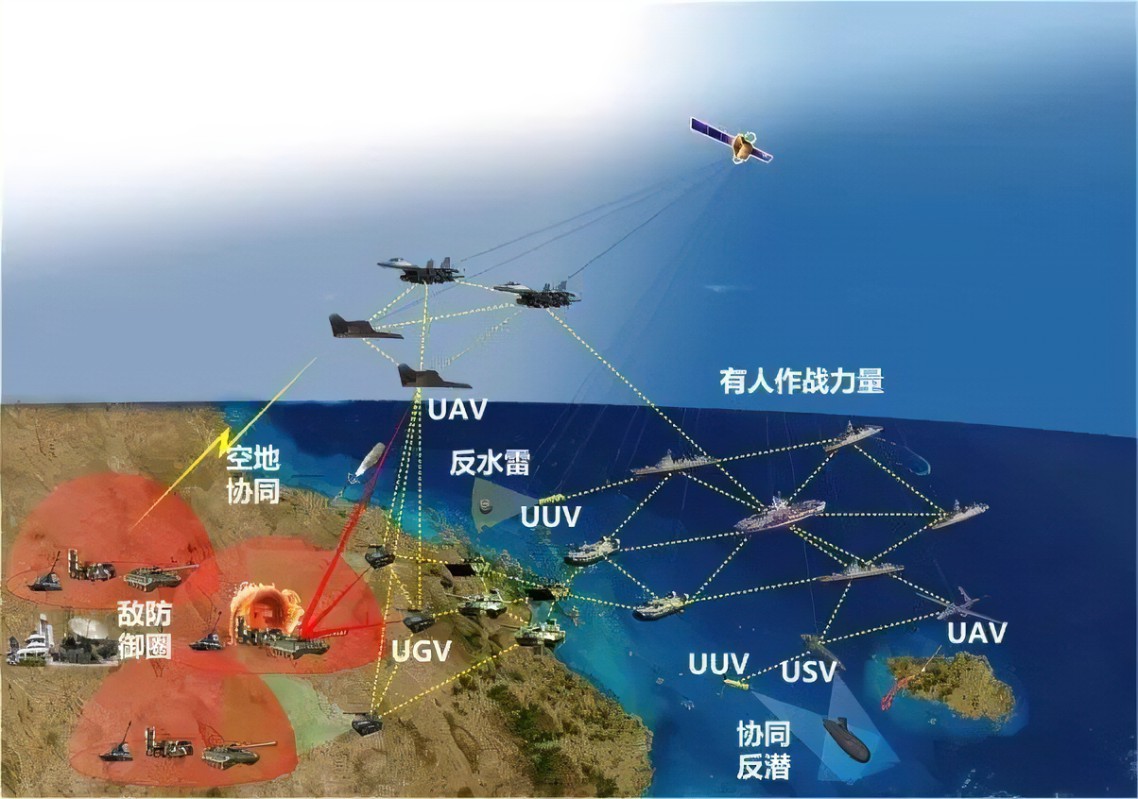
1 脉冲压缩技术的背景

1.1 前备知识

1.1.1 雷达工作原理

雷达，是英文Radar的音译，源于radio detection and ranging的缩写，意为”无线电探测和测距”，即发射电磁波对目标进行照射并接收其回波，由此获得目标至电磁波发射点的距离、距离变化率（径向速度）、方位、高度等信息。

雷达发射机的任务是产生符合要求的雷达波形（Radar Waveform），然后经馈线和收发开关由发射天线辐射出去，遇到目标后，电磁波一部分反射，经接收天线和收发开关由接收机接收，对雷达回波信号做适当的处理就可以获知目标的相关信息。

1.1.2 线性调频（LFM）信号

脉冲压缩雷达最常见的调制信号是线性调频（Linear Frequency Modulation）信号,接收时采用匹配滤波器（Matched Filter）压缩脉冲。

LFM指频率随着时间线性增加（上变频）或减少（下变频）的信号，其复数表达式为：

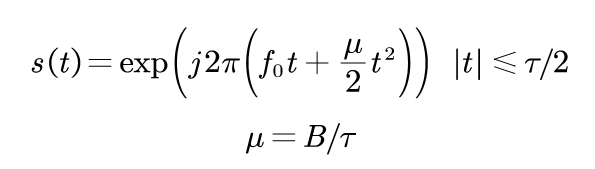
（1）

其中，f0为初始载频，τ为脉宽，u为发射线性调频信号的调频斜率，B为信号带宽。

信号的瞬时频率f (t)为：

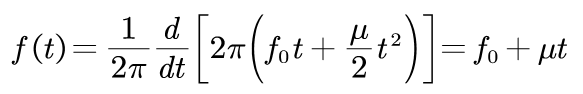
（2）

当B =20MHz，τ=10μ s时，线性调频信号在时域和频域上的波形如下图所示：

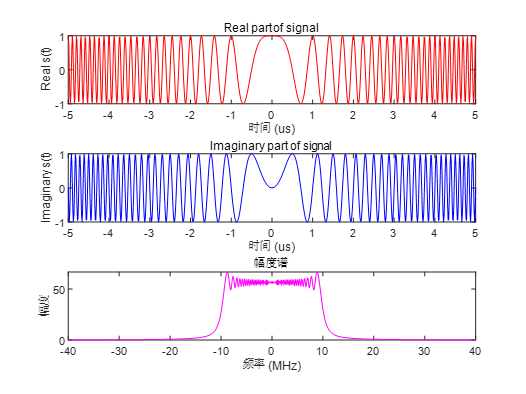
1.2 脉冲压缩的目的和意义

在雷达应用中，对雷达的作用距离、分辨能力、测量精度等性能指标有明确的要求。提高雷达距离分辨能力和测距精度，需要信号具有大的带宽；而提高速度分辨力和测速精度，需要信号具有大的时宽。

雷达最大作用距离指雷达能探测到目标的最远距离，超过这个距离雷达就“看不见”了，雷达只能对在最大作用距离内的目标进行各项参数的估计。雷达的距离分辨率指雷达能够分辨出是两个目标的目标之间的最小距离。如果比这个距离还小的话，雷达就无法判断出那是两个目标。在进行性能优化时，雷达的距离分辨率越小则分辨性能越优。

除此之外，提高雷达系统的作用距离还要求信号具有大的能量，在系统的发射设备峰值功率受限的情况下，大的信号能量只能靠加大信号的时宽得到，这都要求信号具有大的时宽、带宽乘积。由信号与系统理论可知，普通信号的时宽带宽积为一常量，所以信号同时具有大的时宽和带宽是不可能的。而脉冲压缩技术能同时提高雷达的作用距离和距离分辨率。通过采用宽脉冲发射以提高发射的平均功率和雷达最大作用距离；而采用相应的脉冲压缩算法获得窄脉冲接收，以提高距离分辨率，较好的解决雷达作用距离与距离分辨率之间的矛盾。

综上，脉冲压缩使我们在获得相当长脉冲的平均发射功率的同时,能够得到与短脉冲对应的距离分辨率。

2 脉冲压缩技术的原理和公式

脉冲压缩技术主要有两种。第一种技术称为“匹配滤波器”,其被广泛应用于窄带和某些中等带宽的雷达工作中。第二种称为“去斜处理”,通常被用于非常大的宽带的雷达工作中。下面主要介绍前者的原理和公式。

匹配滤波器的原理是将输入信号与一个预定义的模板进行比较，以确定它们之间的相似性。如果输入信号与模板匹配，则输出信号将显示一个峰值，否则输出信号将显示一个低值。

匹配滤波器的公式如下：

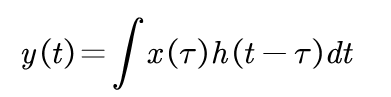
（3）

其中，x(t)是输入信号，h(t)是匹配滤波器的冲激响应。匹配滤波器的输出y(t)是输入信号x(t)与匹配滤波器h(t)之间的卷积。

匹配滤波器接收机带宽B，脉冲持续时间τ，Bτ称为给定波形或其对应匹配滤波器的“时宽带宽积”，表示输出信噪比比输入增加的大小，称为匹配滤波器增益或压缩增益。

一般来说,未调制脉冲的时宽带宽积约等于1。通过使用频率或者相位调制,脉冲的时宽带宽积会远大于1。如果雷达接收机的传递函数理想地匹配输入波形,那么压缩增益等于Bτ。当匹配滤波器的频谱偏离输入信号的频谱时,压缩增益会比Bτ小。

脉冲雷达的雷达方程可以写为

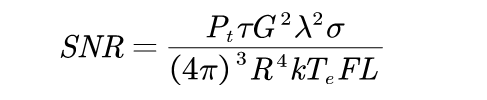
（4）

其中,Pt是峰值功率, τ是脉冲宽度,G是天线增益，o是目标的RCS,R是距离,k是玻尔兹曼常数,Te是有效噪声温度,F是噪声系数,L是总的雷达损耗。

脉冲压缩雷达发射经过调制的相当长的脉冲,然后将雷达回波压缩处理成非常短的脉冲。可以把发射脉冲看做由一系列非常短的子脉冲(占空比为100%)组成,其中每个子脉冲的宽度等于期望的压缩后的脉宽。将压缩后的脉宽表示为τc。因此,对于一个单独的子脉冲,上式可以写成

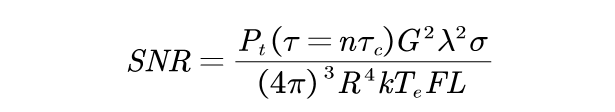
（5）

其中,n是子脉冲的数目。该式被称为脉冲压缩的雷达方程。

对于一组给定的雷达参数,只要发射脉冲保持不变,那么SNR也不变,不管信号带宽如何。更确切地说,当使用脉冲压缩时,通过保持脉宽不变而增加带宽,可以使检测距离不变的同时显著改善距离分辨率。距离分辨率与信号带宽的倒数成正比,即

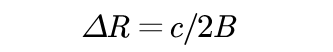
（6）

归一化的复数发射信号形式为：

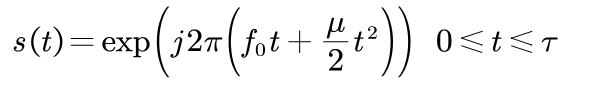
（7）

其中，τ是脉宽，u=B/τ，B是带宽。

雷达从距离为R1的目标接收到的回波信号为：

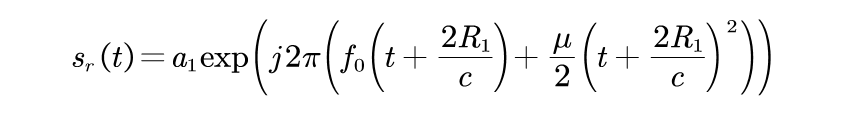
（8）

a1正比于目标的RCS、天线增益及距离衰减。

对于回波信号进行以下处理：

1.消除频率f0

2.对正交分量采样，样本数N的选择必须避免频谱混叠，采样频率需满足奈奎斯特采样定理，才能还原输入信号

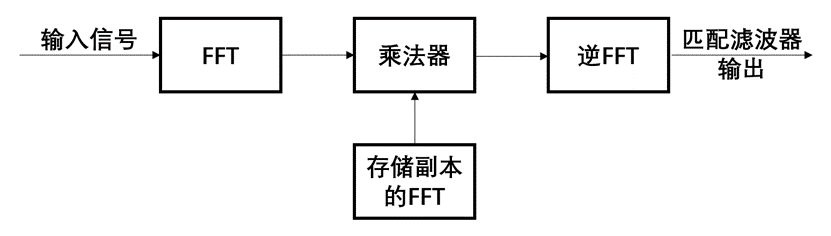
3.快速卷积处理（FCP）步骤包括:(1)对采样序列进行FFT;(2)将信号的频域序列与匹配滤波器冲激响应的FFT相乘;(3)对复合频域序列进行逆FFT,以得到时域压缩脉冲(HRR像)

3 脉冲压缩例程分析与理解

整个程序可拆解为三段。

1、函数中的初始化部分

1	function [y] = matched_filter(nscat,taup,b,rrec,scat_range,scat_rcs,winid)
2	% 函数执行匹配滤波以实现脉冲压缩
3	% 输入
4	    % nscat         == 接收窗口内的散射点数
5	    % rrec          == 接收窗的长度或大小 m
6	    % taup          == 未压缩的脉冲宽度 s
7	    % b             == 信号带宽 Hz
8	    % scat_range    == 散射点的相对位置 m
9	    % scat_rcs      == 散射点RCS矢量 meter squared
10	    % win           == 0 = 不加窗; 1 = 汉明窗; 2 = 带参数pi的凯泽窗; and 3 = 旁瓣为-60dB的切比雪夫窗
11	% 输出
12	    % y             == 归一化的脉冲压缩输出
13	%
14	
15	time_B_product = b * taup;
16	if(time_B_product < 5 )
17	    fprintf('************ Time Bandwidth product is TOO SMALL ***************') 
18	    fprintf('\n Change b and or taup')
19	  return
20	end
21	
22	% speed of light 
23	c = 3.e8; 
24	
25	% number of samples 
26	n = fix(2 * taup * b);
27	
28	% initialize input, output and replica vectors 
29	x(nscat,1:n) = 0.;
30	y(1:n) = 0.;
31	replica(1:n) = 0.;
32	
33	% determine proper window 
34	if( winid == 0.)
35	   win(1:n) = 1.;
36	end
37	if(winid == 1.);
38	    win = hamming(n)';
39	end
40	if( winid == 2.)
41	    win = kaiser(n,pi)';
42	end
43	if(winid == 3.)
44	    win = chebwin(n,60)';
45	end
46	% check to ensure that scatterers are within receive window
47	index = find(scat_range > rrec);
48	if (index ~= 0)
49	    'Error. Receive window is too large; or scatterers fall outside window'
50	  return
51	end

l 第1-13行，定义函数的输入输出；

l 第16-21行，定义了时宽带宽积，并进行初步判断，时宽带宽积太小无法压缩；

l 第23行，定义光速；

l 第26行，定义采样点数，由Nyquist采样定理决定，调用fix函数表示向最近于零取整；

l 第28-31行，初始化输入输出和匹配滤波器响应的向量；

l 第33-45行，定义了四种不同的窗函数；

l 第46-51行，判断散射点是否落在接收窗内。

2、通过解算画出四幅图

1	% calculate sampling interval 
2	f0 = 0 % 载频 
3	t = linspace(-taup/2,taup/2,n); 
4	replica = exp(i * pi *(2*f0.*t+ (b/taup) .* t.^2));
5	figure(1)
6	subplot(221);
7	plot(t,real(replica))
8	ylabel('Real (part) of replica')
9	xlabel('Time in seconds')
10	grid
11	subplot(222);
12	sampling_interval = 1 / 2.5 /b; 
13	freq = linspace(-sampling_interval/2, sampling_interval/2,n); 
14	plot(freq,fftshift(abs(fft(replica))));
15	ylabel('Spectrum of replica')
16	xlabel('Frequency in Hz')
17	grid
18	%接收到三个目标合起来的回波（分辨不出来）
19	 for j = 1:1:nscat
20	    range = scat_range(j);
21	    x(j,:) = scat_rcs(j) .* exp(i * pi * (2*f0.*(t +(2*range/c))+(b/taup) .* (t +(2*range/c)).^2)) ; 
22	    y = x(j,:)  + y;
23	end
24	subplot(223);
25	y = y .* win;
26	plot(t,real(y),'k')
27	xlabel ('相对延迟(s)')
28	ylabel ('未压缩回波')
29	grid
30	% out =xcorr(replica, y);
31	%转换到频域
32	replica_fft = fft(replica,n);
33	y_fft = fft(y,n);
34	%匹配滤波相关运算
35	out_fft = replica_fft.*conj(y_fft); 
36	%转换回时域
37	out = ifft(out_fft,n);%逆傅里叶变换
38	out = out ./ n;
39	s = taup * c /2;
40	Npoints = ceil(rrec * n /s);%采样点和距离（作为横坐标）对应
41	dist =linspace(0, rrec, Npoints);
42	delr = c/2/b;
43	subplot(224);
44	% plot(dist,abs(out(n:n+Npoints-1)),'k')
45	plot(dist,abs(out(1:Npoints)),'k')
46	xlabel ('目标相对位置（m）')
47	ylabel ('压缩后的回波')
48	grid

l 第1-4行，生成线性调频信号，其中f0是载频，n是采样个数，taup/n是采样时间间隔，t是采样时间点构成的向量，根据公式（7）replica是匹配滤波的响应函数即发射信号复制+共轭；

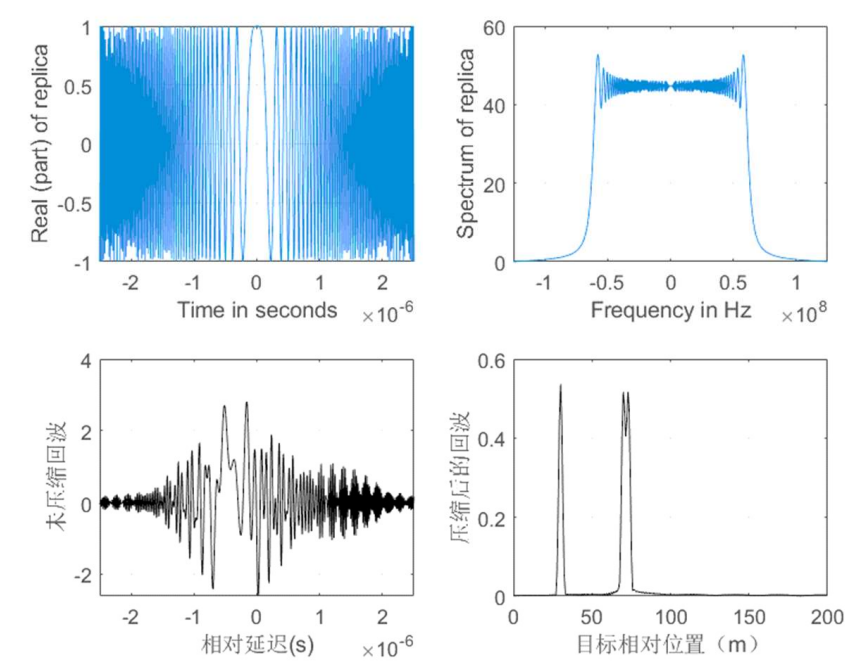
l 第5-10行，画出图1：脉冲压缩中使用副本的实部（时域）；

l 第11-18行，从时域转换到频域，同理画出图2：脉冲压缩中使用副本的频谱图；

l 第12行，Nyquist采样定理规定，频率的步长需大于两倍带宽，这里取2.5倍带宽；

l 第19-30行，图3：未压缩的回波信号（不可分辨）

l 第21行，根据公式（8）是雷达从距离为range的目标接收到的回波信号

l 第32-49行，先通过FFT转换到频域然后进行匹配滤波器相关运算，再转换回时域，将距离作为横坐标画出图4：压缩之后的回波信号（可分辨）

3、调用函数（后续说明）

4 参数变化及思考

4.1 距离分辨率

距离分辨率是区分两个目标信号的最小距离，与信号带宽的倒数成正比，根据公式（6），当信号带宽为100MHz时，理论上距离分辨率值为1.5米，Matlab仿真测出距离分辨率约为2.4米。两个相邻目标信号相聚3米时，可以看到有两个峰值，相聚2米时，只有一个较高的峰值，此时这两个信号无法分辨，且因为回波重叠导致峰值更大。

执行 [y] = matched_filter(3,0.005e-3,100e6,200,[30 70 73],[1 1 1],1);

执行 [y] = matched_filter(3,0.005e-3,100e6,200,[30 70 72],[1 1 1],1);

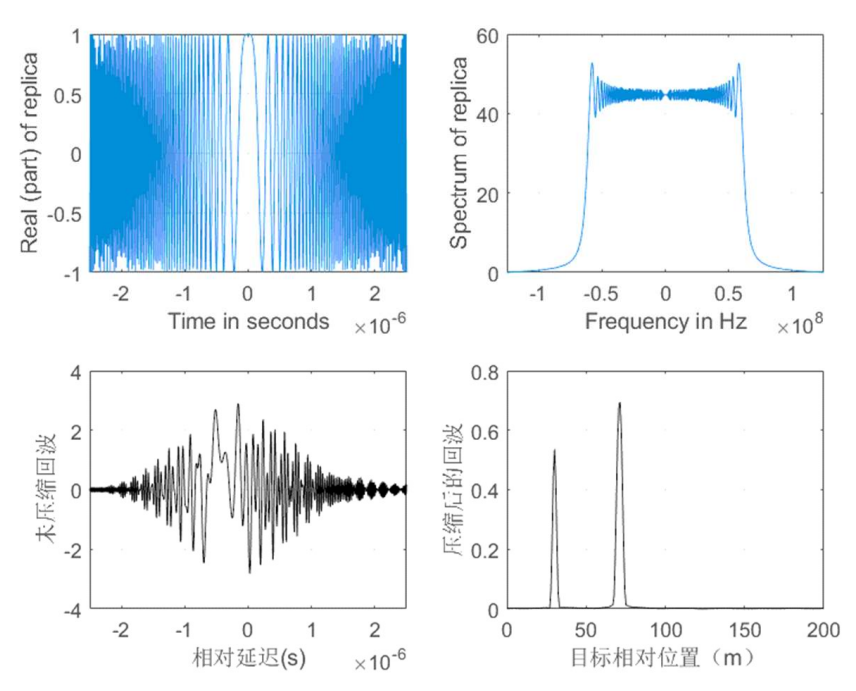
执行 [y] = matched_filter(3,0.005e-3,100e6,200,[30 70 72.4],[1 1 1],1);

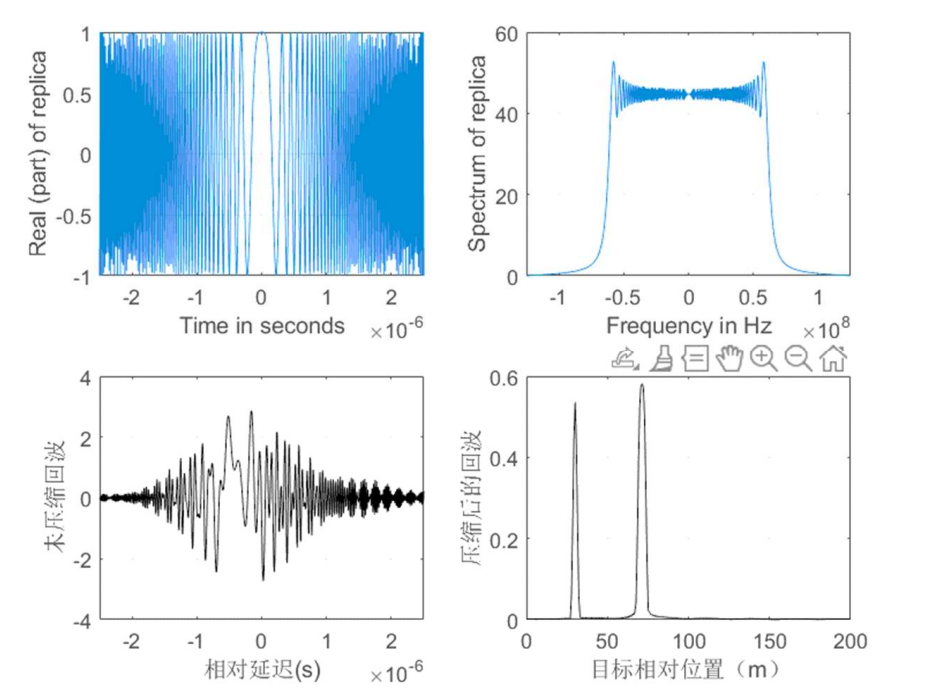
4.2 加窗和接收窗长度

雷达的操作(搜索、跟踪等)通常在规定的距离窗上进行,这个窗称为接收窗,由雷达的最大和最小距离差定义。接收窗内所有目标的回波被接收并且传输给匹配滤波器电路进行脉冲压缩。

另外，使用FFT分析信号的频率成分时，分析的是有限的数据集合。时域和频域都是环形的拓扑结构。时间上，波形的前后两个端点是相连的。如测量的信号是周期信号，采集时间内刚好有整数个周期，那么FFT的上述假设合理。在很多情况下，并不能测量到整数个周期。因此，测量到的信号就会被从周期中间切断，与时间连续的原信号显示出不同的特征。有限数据采样会使测量信号产生剧烈的变化。这种剧烈的变化称为不连续性。这些不连续片段在FFT中显示为高频成分，可能远高于奈奎斯特频率，在0～采样率的一半的频率区间内产生混叠，这种现象叫做频谱泄漏。频率泄漏使好的频谱线扩散到更宽的信号范围中。

加窗可以尽可能减少在非整数个周期上进行FFT产生的误差。数字化仪采集到的有限序列的边界会呈现不连续性。加窗包括将时间记录乘以有限长度的窗，窗的幅值逐渐变小，在边沿处为0。加窗的结果是尽可能呈现出一个连续的波形，减少剧烈的变化。

窗的波形图显示了窗本身为一个连续的频谱，有一个主瓣，若干旁瓣。主瓣是时域信号频率成分的中央，旁瓣接近于0。旁瓣的高度显示了加窗函数对于主瓣周围频率的影响。对强正弦信号的旁瓣响应可能会超过对较近的弱正弦信号主瓣响应。一般而言，低旁瓣会减少FFT的泄漏，但是增加主瓣的带宽。旁瓣的跌落速率是旁瓣峰值的渐进衰减速率。增加旁瓣的跌落速率，可减少频谱泄漏。

每一种加窗函数都有其特征和适用范围。要估计信号的频率成分以选择加窗函数。窗函数的选择可以参考下表。

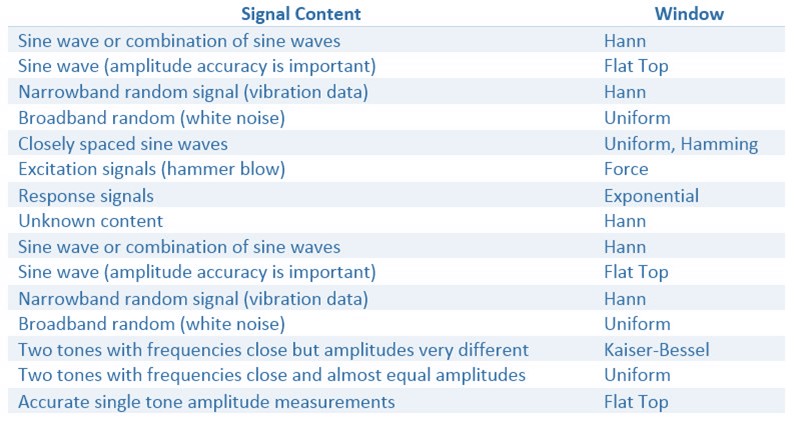
即使不使用任何窗，信号也会与高度一致的长方形窗进行卷积运算。本质上相当于对时域输入信号进行截屏，对离散信号也有效。该卷积有一个正弦波函数特性的频谱。所以，没有窗叫做统一窗或长方形窗。

本例中，汉明窗和旁瓣为-60dB的切比雪夫窗效果较好。

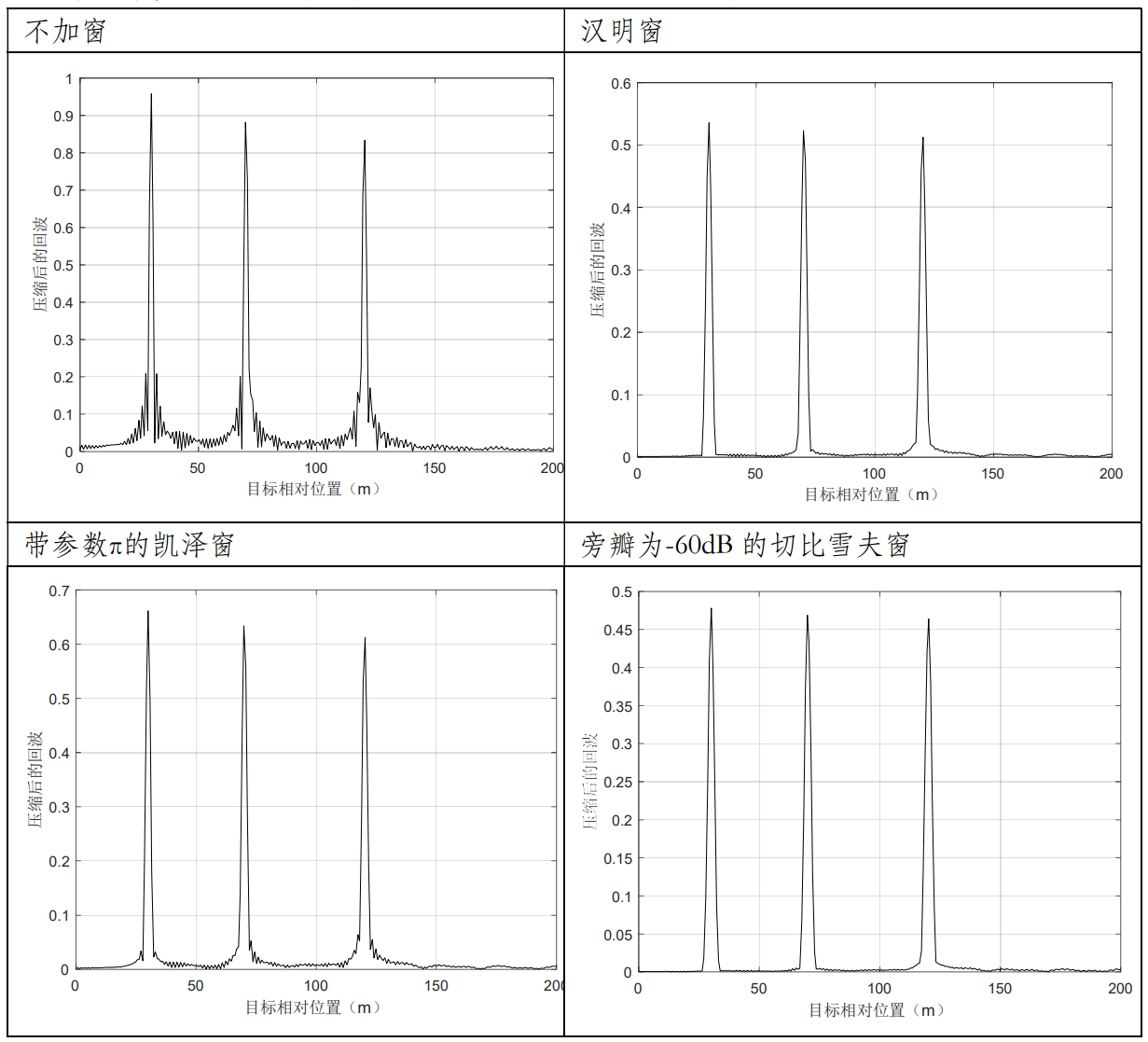
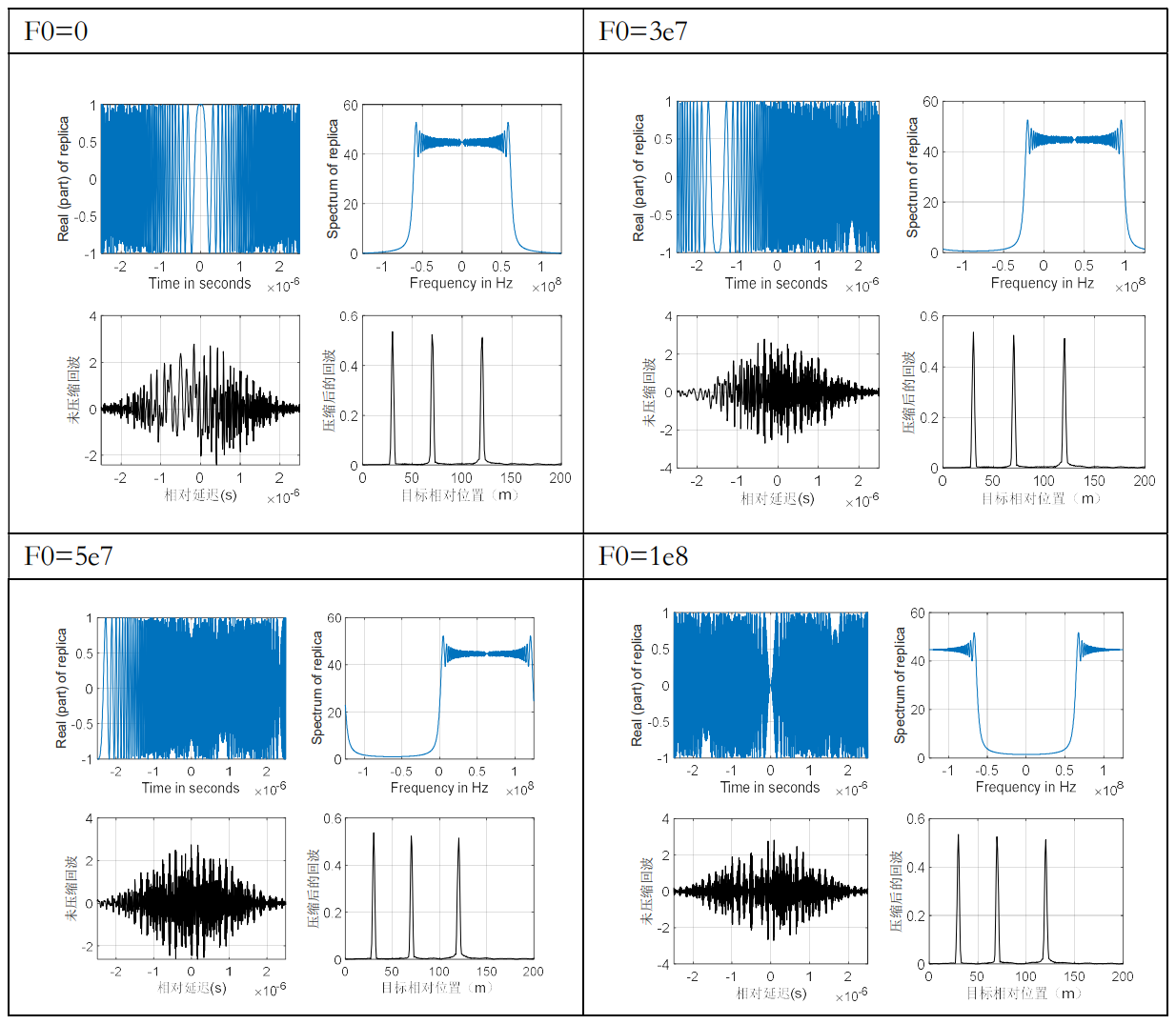
4.3 载频变化

载波是指被调制以传输信号的波形，一般为正弦波。载波信号，就是把普通信号（声音、图像)加载到一定频率的高频信号上，在没有加载普通信号的高频信号时，高频信号的波幅是固定的，加载之后波幅就随着普通信号的变化而变化(调幅)还可以调相，调频。载波信号─般要求正弦载波的频率远远高于调制信号的带宽，否则会发生混叠使传输信号失真。

载波信号的作用包括:

1、减小传输中的噪声;

2、频分复用，即同一频率之间同一信道传输多路信号而不混叠;

3、可传播更远距离，有利于接收。

图上表现在发射信号在时域和频域中心频率的偏移，未压缩的回波信号也有所不同，但对压缩之后的回波信号没有什么影响，这与前文提到的对回波信号进行消除f0的处理有关。

4.4 RCS变化

雷达散射截面积(Radar Cross Section, RCS)是目标在雷达接收方向上反射雷达信号能力的度量，一个目标的RCS等于单位立体角目标在雷达接收天线方向上反射的功率(每单独立体角)与入射到目标处的功率密度(每平方米)之比。

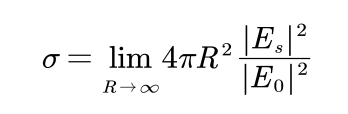
（9）

对于一般物体的RCS如下表：

目标类型	RCS /m²
昆虫或鸟类	1e-5 ~ 1e-2
人类	0.5 ~ 2
飞机	1 ~ 100
汽车或火车	100 ~ 300
轮船	200 ~ 1000

对于隐身飞机，采取多种措施，使镜面反射和边缘绕射基本消失。典型的战斗机的雷达散射截面积(RCS)约1平米，而“隐身飞机”的RCS仅为0.01平米，甚至更小。

执行 [y] = matched_filter(3,0.005e-3,100e6,200,[30 70 120], [0.01 0.5 5],3); 当目标RCS小于0.1时回波几乎不可发现。

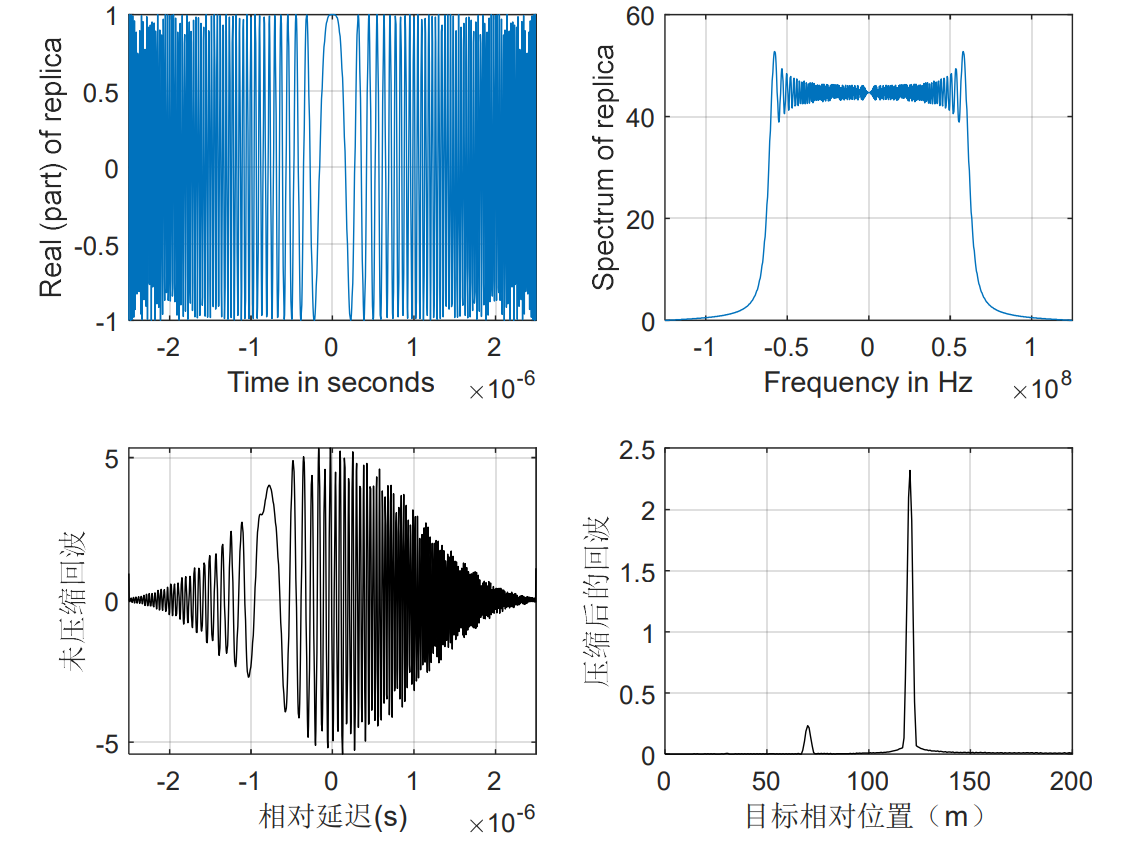
4.5 目标速度

当目标有速度时（假设为匀速），构建matched_filter_move函数，添加scat_speed为散射点的速度的输入变量,将range = scat_range(j);替换为range = scat_range(j)-scat_speed(j)*t;

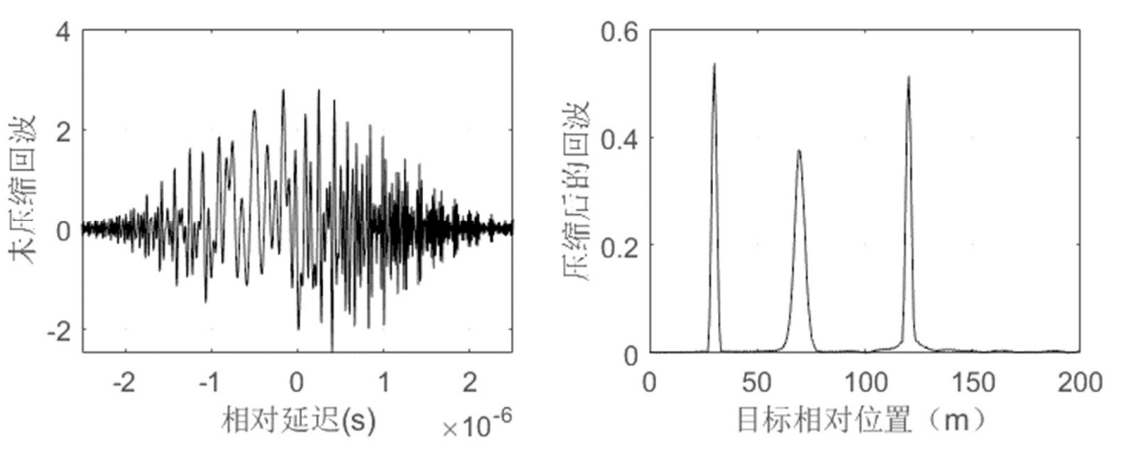
执行 [y] = matched_filter_move(3,0.005e-3,100e6,200,[30 70 120],[0,1000000,0],[1 1 1],1);

由图可见，给相对位置为70的目标一定速度，该目标的回波峰值减小而宽度变大，即因为目标有运动速度，其位置在70附近的概率增大。

4.6 匹配滤波器和去斜处理的对比

去斜处理Stretch方法是针对线性调频信号而提出的，其方法是将输入信号与参考信号（经适当延迟的本振信号，延迟量通常由窄带信号测距结果估计出）混频，则每一个散射点就对应一个混频后的单频分量，对混频输出的信号进行DFT处理，即可获得目标的距离像，对参考信号的要求是应具有与输入信号相同的调频斜率。混频过程为回波信号在时域与参考信号的共轭相乘，混频后得到一个瞬时频率和目标距离成正比的单频信号，对其进行频谱分析即可得到目标的距离像；去斜处理一般情况下可降低信号带宽。

理论上，带宽小时匹配滤波器和去斜处理结果相同，带宽大时两者不同，去斜处理更适用于带宽较大的情况。下面对几种情况进行仿真，探寻去斜处理更适用于带宽较大的信号的原因。

带宽较小时（1e8）：

匹配滤波器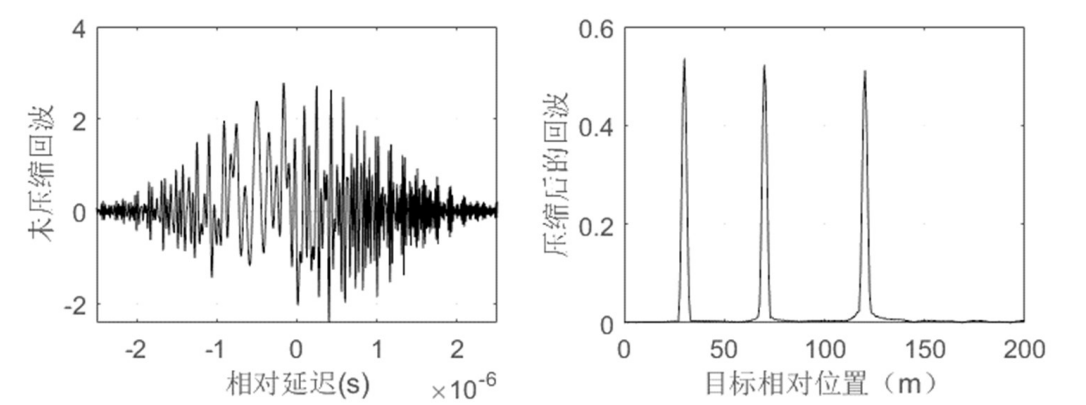

去斜处理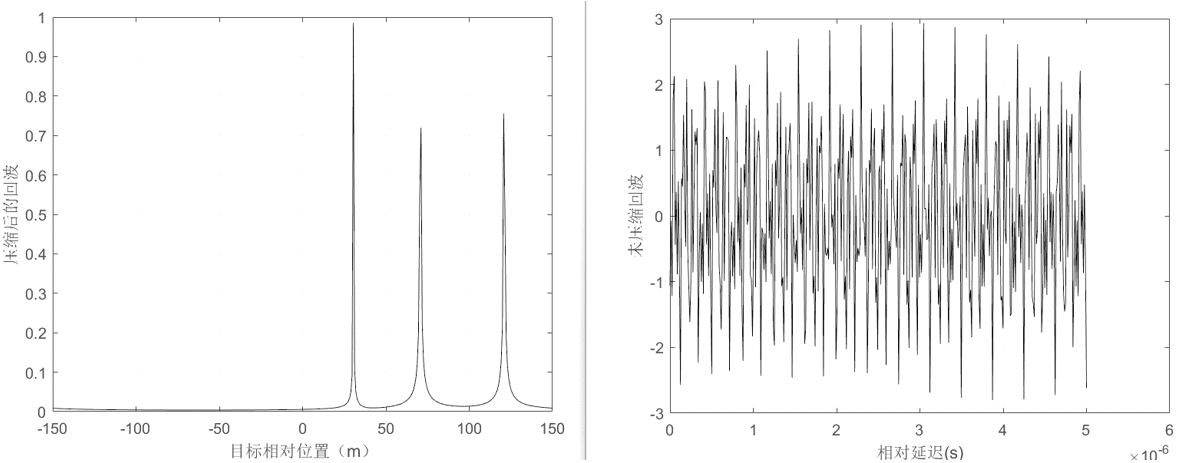

带宽较大时（1e10）：

匹配滤波器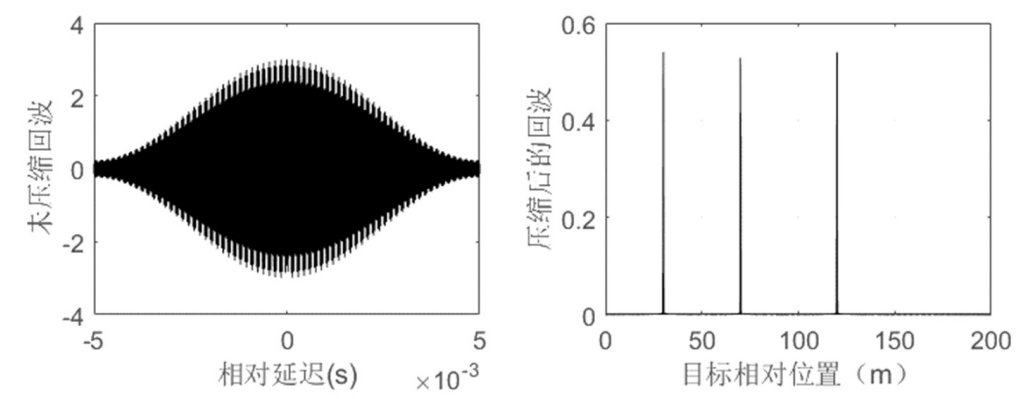

去斜处理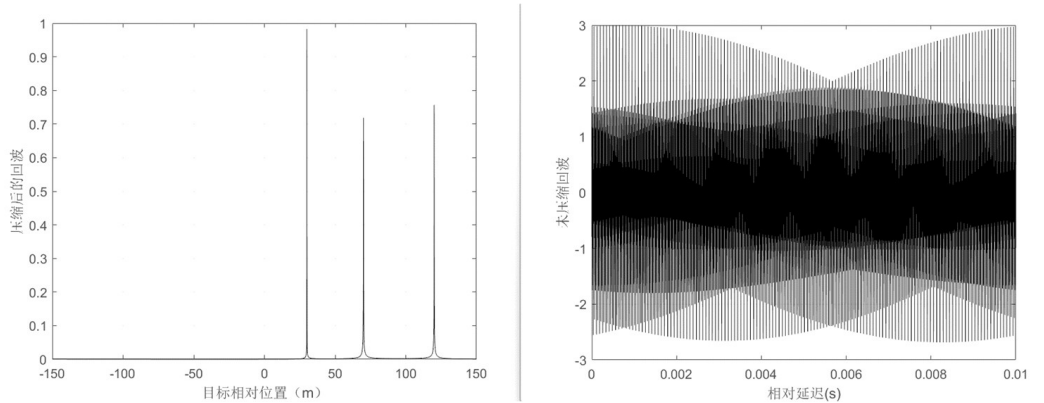

带宽更大时：（taup不变 带宽更大为1e11）

匹配滤波器：出现内存不足的现象，问题在于“采样点数太多” 减小taup为10e-6可以 结论：如果直接采样的话因为频带很宽所以在高频的时候需要的采样率就很大，采样点数就很多，所以要经过去斜处理。 执行 [y] = matched_filter(3,10e-3,1e11,200,[30 70 120],[1 1 1],1);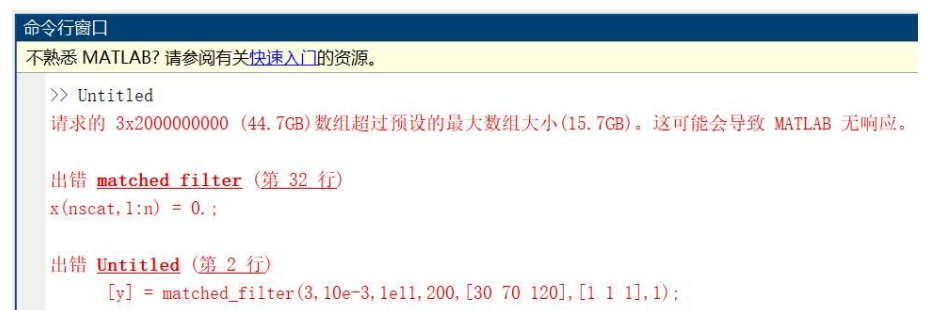

去斜处理在相同的参数下，可以正确执行，证明其更适用于时宽带宽积更大的信号。 执行 [y] = stretch(3,10e-3,5.6e9,1e11,300,[30 70 120],[1 1 1],1);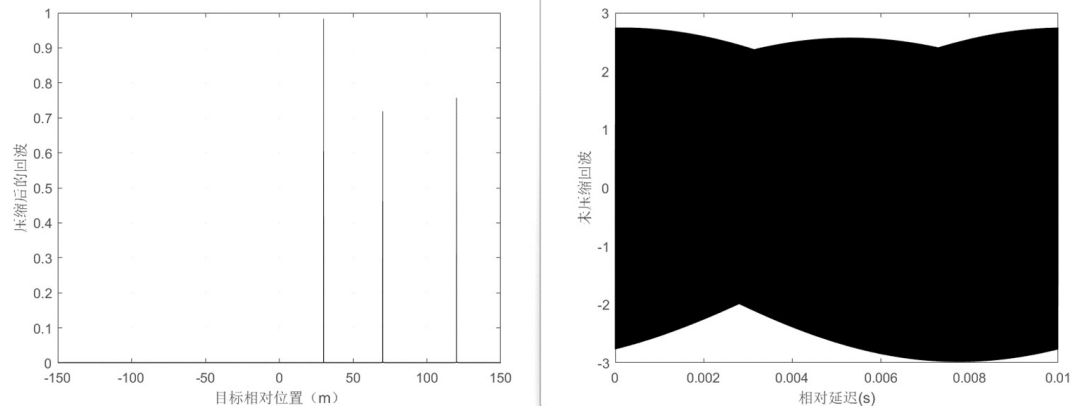

参考文献

[1] 许小剑，黄培康，雷达系统及其信息处理（第2版），电子工业出版社，2018.

[2] https://blog.csdn.net/wangjie36/article/details/115803471

[3] https://blog.csdn.net/nidetianmei33/article/details/127983795

[4] https://blog.csdn.net/liu010609/article/details/119543873