摘 要:在多无人机协同工作,特别是作战过程中, 任务规划技术是多无人机协同应用的顶层设计,属于带约束的组合优化问题,是在任务需求、单元能力和环境态势的影响下,优化求解获得满足要求的任务执行方案,对无人机能否形成高效的配合至关重要。本文研究总结了多无人机在任务规划方面的发展现状和关键技术,阐述了任务分配、路径规划的主要过程和算法,分析了不同算法的特性及适用性, 并列举了研究者们对部分算法的改进。然后以具体算法为例,介绍聚类经典算法K-means的基本原理以及在任务规划中的应用,不仅能实现多无人机-多目标分配,还能配合其他算法完成多航迹规划,以应对突发状况。最后对多无人机协同任务规划做了总结和未来发展方向的预测。
关键词:多无人机协同系统;任务分配;航迹规划;聚类算法;综述
A Review of Research on Multi-UAV Collaborative Mission Planning
Abstract: In the multi-UAV cooperative work, especially during combat, the mission planning technology is the top-level design of multi-UAV cooperative application, belonging to the combinatorial optimization problem with constraints, which is to optimize the solution to obtain the mission execution scheme that meets the requirements under the influence of the mission demand, unit capability and environment situation, and it is crucial for the UAVs to be able to form efficient cooperation and play positive effect. This paper summarizes the development status and key technologies of multi-UAVs in mission planning, describes the main processes and algorithms of task allocation and path planning, analyzes the characteristics and applicability of different algorithms, and lists the improvements of some algorithms by researchers. Then specific algorithms are taken as examples to introduce the basic principle of the classical algorithm of clustering, K-means, and its application in mission planning, which not only realizes multi-UAV-multi-target assignment, but also cooperates with other algorithms to complete multi-trajectory planning to cope with unexpected situations. Finally, the multi-UAV collaborative mission planning is summarized and the future development direction is predicted.
Key words: Multi-UAV collaborative system; Task allocation; Path planning; Clustering algorithm; Review
0 引 言
近年来需求和科技的蓬勃发展推动着无人机的应用落地生根、研究也更进一步,因具有续航时间长、生存力高、机动适应性强、隐蔽性好等特点,无人机被广泛应用在军事上靶机、侦查、攻击,民用上交通、农业、航拍等多种任务场景。
当前大型全能型无人机(如“死神”无人机、“全球鹰”无人机等)系统集成度高且功能强大,但面对日益复杂的任务需求,仍存在任务效费比低、系统容错性差和升级周期长等缺陷。多无人机系统旨在将大型平台的功能分散到空间分布的大量无人机,利用网络连接这些功能相对单一的低成本单元,通过合理调度实现不同单元的动态组合和密切协作,能够在兼具经济性的基础上达到甚至超过大型平台能力水平,实现以量取胜。
多无人机系统具有单元配置灵活、部署形式多样、任务能力全面、系统冗余度高和经济成本低等优势,可以极大提升未来战场的不对称优势,国内外都积极开展了相关研究工作。
美国方面,美国防部战略能力办公室 (SCO) 2014年实施拒止环境中的协同作战项目(CODE),着眼在高强度军事对抗下,使得无人机具备更好的自主作战能力。通过有人机空射“灰山鹑”微型无人机蜂群执行低空态势感知和干扰任务,该“蜂群”作战系统突出数量大、低成本和机载发射等特点,已经成功完成了103架无人机集群组网以及编队飞行的技术验证。美国国防预先研究计划局(DARPA)于2015 年推出“小精灵”项目,计划研制具备自组织和智能协同能力的无人机蜂群系统,注重机载平台发射以及自主回收技术,以进一步降低作战成本以及有人空中平台的战损概率。 美国海军研究局(ONR)于2015 年公布了“低成本无人机蜂群” (LOCUST) 项目,研发可快速连续发射的无人机蜂群,无人机之间利用近距离射频网络共享态势信息,协同执行掩护、攻击或防御任务。2017年,DARPA 会议中心举办“进攻性集群战术” (OFFSET)项目,计划实现一个步兵部队控制250多个无人机与无人地面系统组成的异构无人系统在有高大建筑、机动、通信受限的城市作战环境中进行协同作战。


欧洲方面,2016 年,欧洲防务局启动了“欧洲蜂群”项目,开展了无人机蜂群的自主决策、协同飞行等关键技术研究。 2016 年,英国国防部发起无人机蜂群竞赛,参赛的多个团队控制无人机蜂群实现了通信中继、协同干扰、目标跟踪定位和区域测绘等任务。2017 年,俄罗斯无线电电子技术集团对外发表研究计划称,在战斗机上装载多架蜂群无人机可实现协同侦察和攻击的新型作战样式[1]。
国内也相继展开相关研究。2017年,北京航空航天大学研制的“天鹰”无人机具备与有人作战飞机联合作战的技术。2020年,中国电科集团(CETC)电子科学研究院公布了一段陆空协同固定翼无人机“蜂群”作战系统的演示视频,展示了车载快速部署、密集发射、空中悬停投放、机动投放、精确编队、阵型变换、对地察打、精确打击等全流程任务能力,一次最多可以投射200架。


这些项目都离不开及时有效的任务分配和后续精确的航迹规划,美军“分布式空中作战”概念更是印证了这一观点,提出创建一支灵活组合的异构有人/无人作战编队,将不同种类的无人机依据任务按需变成侦、控、扰、打、评等作战单元。其中,隐身高价值载荷无人机如RQ-170、RQ-180等可在中低威胁空域担负作战任务。中等价值无人平台如XQ-58A等在中等威胁空域活动,作为通信节点、控制节点和前方火力发射平台,配合前方无人机和后方有人机编队作战。较低成本的“小精灵”无人机则搭载侦察、干扰、反辐射、战斗部等多样化任务载荷,在高威胁空域实施作战。低成本巡飞弹如“弹簧刀”“郊狼”等,限于自身航程限制,担负外围防空压制任务,以自身数量优势饱和对方防空通道、消耗其防空弹药。
多无人机协同任务规划即是根据一组特定条件的约束,以实现某个准则函数的最优或次优为目标,将某项任务分解成一系列子任务并分配给多无人机系统中的各个无人机分别去完成的过程。 通常可以分成两大部分:上层的任务分配(Task Allocation)和下层的路径规划(Path Planning)。同时,多无人机协同任务规划系统本身又是整个协同控制系统的重要组成部分。
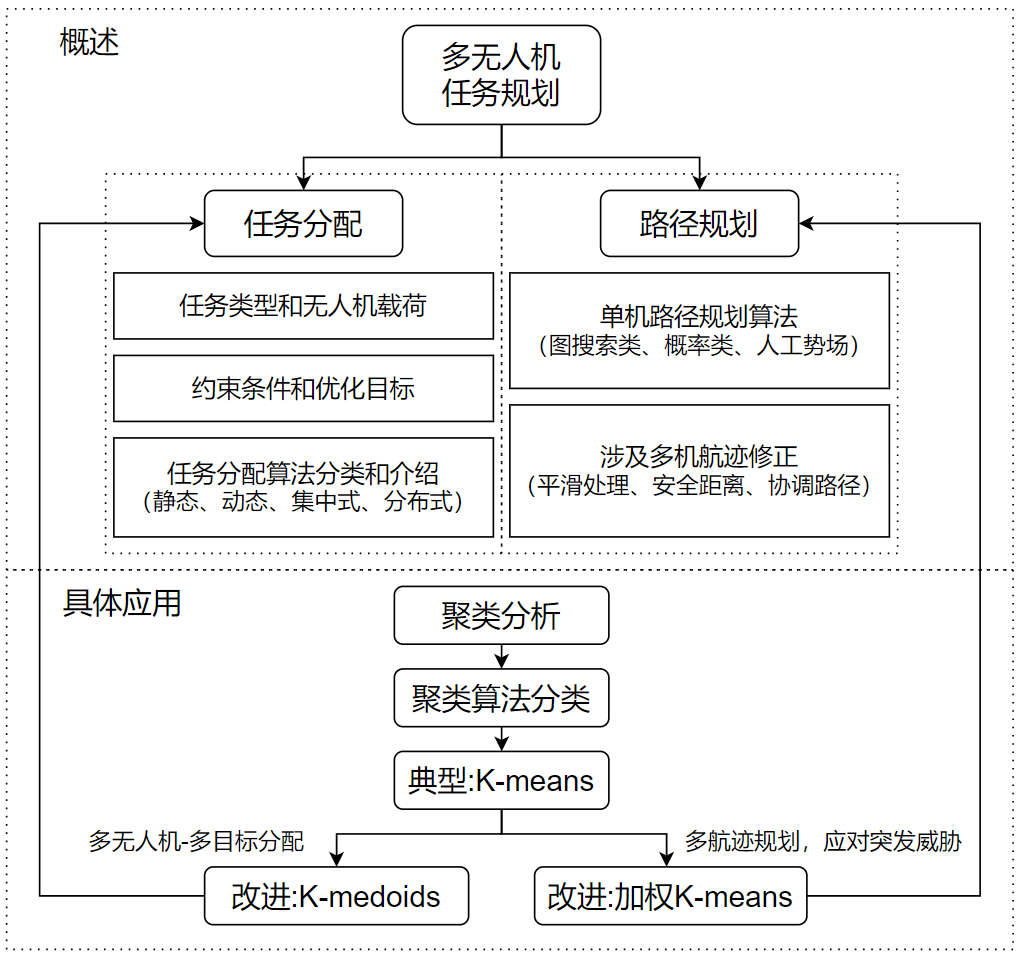
面对这一重要课题,本文研究总结了多无人机在任务规划方面的发展现状和关键技术,首先分别概述了任务分配、路径规划的主要过程和算法,然后以具体算法为例,介绍聚类经典算法K-means的基本原理以及在任务规划中的应用,最后对多无人机协同任务规划做了总结和未来发展方向的预测,论文整体框架如图3所示。
1 任务分配
任务分配是考虑各种约束条件,以有效达成总体任务为目标,将具体目标和行动任务分配给各机,而各机根据分配的任务再进行具体的路径规划。
1.1 任务类型与无人机载荷
将不同任务分配给各无人机时,需要考虑两者的匹配程度,常见任务类型如下:
1)覆盖搜索:对大面积未知区域进行持续性监视,确定其内部目标信息,包含行为式覆盖(Z 型、回型)和非行为式覆盖[2,3,4]。
2)定点侦察:采用不同类型的任务载荷(光学、红外或雷达等)对位置概略已知的目标进行多层次的信息收集。
3)目标追踪:对区域内移动目标进行持续监视,为后续任务提供信息支撑。
4)火力打击:使用多类型武器对信息已知的目标进行毁伤,同时多向打击可以有效提升打击成功率[5]。
5)效果评估:对完成打击任务的目标进行评估,判断是否达到毁伤要求[4,6]。
6)通信中继:为通信能力有限的无人机提供通信连接,扩展无人机任务范围。
7)物资运输:将充足数量和指定类型的物资运输到目标点[7]。
8)电子干扰:实施电子压制降低对方探测和打击能力[8]。
通常根据任务需求和无人机能力调整任务设置。文献[9]区分防御高和防御低的目标,针对防御高的目标增加打击任务数量,以确保毁伤效果。文献[10]针对无人机潜在断连风险,派遣中继无人机执行通信中继任务,使得无人机可在基站通信范围外执行观测任务。文献[11]针对应急区域覆盖搜索,根据目标位置、区域大小和无人机续航调整任务设置,能够兼顾任务效果与无人机负载。
多无人机系统单元间的差异主要体现在动力学性能和载荷功能两方面。
动力学性能影响任务路径设置和到达时间计算,在任务规划计算时主要考虑速度范围、转弯半径、最大爬升角和最大下滑角等限制,部分研究进一步简化为二维空间的速度与转弯半径限制。设任务场景包含N架无人机,则二维笛卡尔坐标系下无人机的运动学模型为[12]

载荷功能影响任务指派和效果评估,此处针对常用的侦察、打击和通信载荷进行分析[49]:
1)侦察载荷:从目标发现角度可简化为搜索半径,或通过视场角与飞行高度计算扫描范围。针对目标识别问题,单传感器侦察需考虑置信概率,多传感器协同侦察需考虑信息融合问题。
2)打击载荷:从目标毁伤角度一般简化为打击范围和毁伤概率指标。
3)通信载荷:一般简化为通信半径,即该范围内单元相互连接[13,14],进一步考虑通信拓扑结构[15,16]、通信跳数[16]、路径损耗和接入单元数量[17]等限制。
多无人机系统可以通过平台与载荷的灵活配置,形成多样化的任务能力。合理的配置方案可以提升机间协同效率,在满足任务需求的同时避免资源浪费。
1.2 约束条件
任务分配模型约束可分为任务相关类和无人机相关类,具体如下。
1)任务时序耦合约束:不限制任务的具体执行时间,但限制任务间的相对执行顺序,可分为同时执行、前序执行、后序执行、任务间执行和任务互斥五类[18,19],可以使用有向无环图进行精确描述[20]。忽视该类约束会出现“死锁”问题并产生无效解[21]。可以通过任务分层计算[18]、强连通量消除[20]和关联任务打包编码[4,21]等方法处理。
2)任务时间窗约束:限制任务的具体执行时间(最早开始/最晚结束),根据违约处理策略可分为硬时间窗和软时间窗两类。在时间窗限制下,到达过早需要“等待”,到达过晚会受到惩罚或错失任务[19],其中的“等待”过程降低了速度不确定性对任务执行的干扰。
3)无人机数量约束:参与任务执行的某一类型无人机数量不能超过数量限制,主要出现在无人机配置可变的场景。例如侦查任务,派出无人机数量越多,越容易被发现,故需要进行数量约束。
4)无人机航程约束:无人机所携带的能源有限,部分场景需要考虑返航需求。一般使用燃料消耗、飞行距离、飞行时间和最大任务数量等指标进行计算。
5)无人机能力约束:无人机必须具有相应能力方可执行任务。载荷能力可以使用 0-1 变量进行简要判断,或结合功能半径和执行概率等参数进一步建模。
约束数量随问题规模变大呈非线性增加,大部分约束只涉及单架无人机或部分任务,少量约束则涵盖全部任务与无人机,约束之间耦合关系复杂。对此,可以使用惩罚策略[21]、放松策略[19,21]和构造修补策略[22]等进行处理。
1)惩罚策略:根据违约情况调整模型优化目标值,将原始约束问题转化为无约束问题求解,在约束较少的情况下筛选可行解的效率高,但在大规模约束情况下可能无约束解很少[21]。
2)放松策略:在可接受范围内先放松部分约束,后续根据需求进一步增加限制。放松约束可能导致解的性能下降,但可以有效提升求解效率,增强解的多样性。文献[21]为避免调整“死锁”带来的巨大时间成本,设计了成本近似函数以替代调整过程,虽然降低了结果性能,但大大缩短了求解时间;文献[23]针对时序耦合场景,构造包含少量约束的主问题,然后动态增加对优化目标有改进的约束条件,有效缩短了多约束问题的计算时间。
3)构造修补策略:根据约束关系设计多种类型的操作,对违约解进行调整,能够确保最终解的可行性,但调整多类约束的操作复杂。文献[22]针对时序耦合、动力学和能力等约束,调整编解码生成无“死锁”方案,设计了无人机选择算子以满足能力约束,以Dubins曲线设计任务路径并协调到达时间,通过多次调整生成可行解。
1.3 优化目标
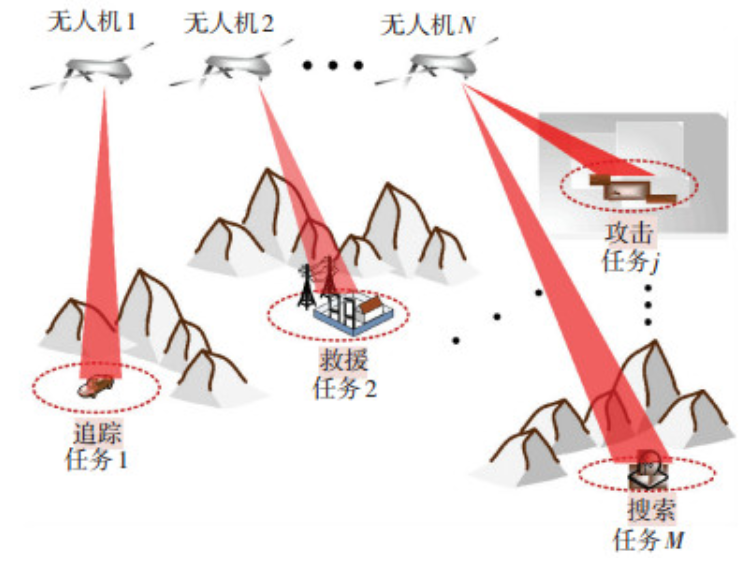
假设任务控制场景中有M项任务,如图4所示,任务分配的目标为最大化全局目标函数,实现任务到无人机的无冲突分配,假设每个任务只分配给一架无人机,每架无人机可执行多个任务。任务分配问题的全局目标函数为


1.4 任务分配算法及分类
任务分配是一个有约束条件的多目标优化问题,按照任务分配的时间可以分为静态、动态任务分配策略,按照任务分配的主体可以分为集中式和分布式。
1.4.1静态任务分配
静态任务分配方法在多无人机系统中发挥着基础作用。这种方法通常在任务开始之前根据预先确定的信息来分配任务,算法通常考虑无人机的数量、任务类型、地理位置和其他静态参数。经典的静态分配方法包括线性规划、整数规划和分支限界法等。这些方法试图找到在给定约束条件下的最优解。在实际应用中,通常适用于任务和环境参数相对固定的情景,如定期的监控任务或标准化的数据收集工作,但它们无法适应快速变化的任务需求。
1.4.2动态任务分配
动态任务分配方法在多无人机系统中用于实时调整任务和路径规划,以应对环境的不断变化。这些方法通常基于先进的算法,如遗传算法、粒子群优化和强化学习。例如,遗传算法通过模拟自然选择和遗传机制来找到最优的任务分配方案。粒子群优化通过模拟鸟群或鱼群的社会行为来优化解决方案。强化学习则允许无人机通过与环境的交互来学习和改进其行为。这些算法的关键在于它们能够处理大量的动态信息并快速做出决策,从而提高多无人机系统的灵活性和效率。
1.4.3集中式方法
集中式方法利用中心节点收集信息并指派任务,可以充分协调各类资源,获得最优方案,但是依赖于中心节点且扩展性差, 适用于任务执行前综合已知信息进行调度。常用的模型有多旅行商问题(Multiple Traveling Salesman Problem ,MTSP)模型、车辆路径问题(Vehicle Routing ,VRP)模型、混合整数线性规划问题(Mixed-Integer Linear Programming, MILP)模型、动态网络流优化(Dynamic Network Flow Optimization ,DNFO)模型等。
针对的求解算法有最优化方法,例如穷举法、整数规划法、约束规划法、图论方法。网络流模型和偶图匹配模型是两种经典的图论任务分配模型。也有启发式算法,在能够接受的时间范围内求得局部最优解或满意解,如进化算法(evolution algorithm,EA)、遗传算法 (genetic algorithm,GA)和粒子群算法(particle swarm optimization,PSO)等。文献[24]分析了无人机配置与任务分配的关联关系,设置了基于进化算法的双层求解方法,结合任务分配计算情况调整无人机数量,可以获得精确的无人机配置方案。文献[4,22]基于改进遗传算法求解任务规划,使用多层目标束编码建立无人机与任务的映射关系,改进交叉和变异操作以增强搜索能力。文献[21]使用狼群算法求解,使用两段式编码降低搜索空间,引入新的换位和扩展操作以增强搜索能力。该类方法需要将问题空间合理映射至算法空间,动态调整控制参数以平衡全局搜索与精细调整[25,26],恰当处理多类约束以平衡求解效率与可行性[27],融合不同更新操作以增强搜索能力[28,29]。
1.4.4分布式方法
分布式算法基于去中心化思想设计,依赖于机间信息交互实现任务协同,避免了单点失效风险且扩展性较好,但缺少中心节点的协调会造成单元间的任务竞争,适用于在任务执行中根据场景变化快速调整方案,对无人机的要求更高,需要具备独立计算、分析与决策等能力。
分布式算法可分为市场协商方法、分布式约束优化方法和多智能体类方法三类:
1)市场协商方法根据“拍卖-竞标-中标”竞拍机制将任务分配给“收益”最高的单元,为单个任务[30]或多个任务[31]选择合适执行单元,其代表性算法包含拍卖算法[21]、合同网算法[32]、一致性众包算法[33,31]和性能评估算法[34]等;
2)分布式约束优化方法是将任务列表在单元间传递,任务满足“选择阈值”则进行分配,更依赖于单元本地信息进行决策,协调通信需求低,其代表性算法包含Swarm-Gap 算法、令牌传递算法和 Max-Sum 算法等;
3)多智能体类方法是赋予各单元信息收集与分析能力,以集群涌现的形式实现任务协同。群体智能算法侧重对生物群体机制的学习,如鱼群迁徙、狼群捕猎、蚁群搬运和蜂群觅食等。
2 路径规划
路径规划是在满足如最大线性速度、最大转角速度、操作的安全性、时间和环境变量等自身或外部限制的前提下,在一系列航迹点之间设计或生成路径。为降低问题复杂性,多采用分层规划的思想,首先根据已知的环境信息、任务要求等在无人机起飞前为其规划出一条满足约束条件的全局最优参考航迹。无人机在按照此航迹飞行的过程中,当出现未知或动态威胁信息时,再进行局部航迹动态优化。由于全局参考航迹规划需要考虑整体的优化,因此要在避免陷入局部最优的情况下尽量减少计算量。而局部航迹动态优化用于应对突发威胁,因此要尽量缩短规划时间以确保实时性[35]。多无人机相比单无人机还要考虑时序问题、航迹修正和安全距离等,防止相撞。
2.1 单机航迹规划方法
单无人机航迹规划一般由以下几个部分组成: 描述规划空间,选择航迹的表示形式,分析约束条件, 确定代价函数,选取航迹搜索算法和航迹平滑。
根据空间离散策略的不同,单机航迹规划方法可分为图搜索类方法、概率类方法和人工势场法三类,相关方法对比见表1。
1)图搜索类方法:将任务空间离散成连接目标和障碍的路径网络,在此基础上搜索获得最/较优路径。常用空间离散方法包含可视图法、Voronoi 图法和栅格法等;常用搜索方法包含 Dijkstra 算法、A*算法、动态规划、元启发算法和强化学习等。不同离散方法和搜索方法的组合可以适应不同任务需求:文献[36]针对城市内未知移动目标搜索场景,使用 Voronoi 图法设置待选航路点,使用滚动时域预测方法优化路径,可以兼顾飞行安全和搜索效率。文献[37]针对不确定区域内的搜索打击场景,使用栅格法离散区域,通过分布式蚁群算法优化路径,可以有效引导无人机搜索目标存在概率高的区域。
2)概率方法:在任务空间中设置大量采样点,使用直/曲线连接起点、部分采样点与终点形成任务路径,通过优化连接采样点提升路径质量。根据采样点设置策略不同分为概率路标图法和快速随机树法。该类方法不需要对场景进行建模,对动态或多障碍场景适应性很好,能够快速得到可行路径,但受采样点设置和搜索策略影响路径较为曲折。文献[38]利用快速随机树法处理未知障碍或突发威胁,能够快速调整现有路径绕过障碍区域。
3)人工势场法:在任务空间建立虚拟力场,叠加目标产生的引力与障碍产生的斥力,生成靠近目标且远离障碍的路径。该方法原理简单,可以引入敌方火力威胁、相邻无人机等多类因素,有效提升任务路径的安全性。但是力场函数设置不合理时可能产生无法到达目标、违反避障约束和局部震荡等问题,对此发展了多种改进策略,如距离修正、局部扰动等[39,40]。
| 名称 | 内容 | 优缺点 |
|---|---|---|
| 可视图法 | 连接起始点、目标点和多边形障碍顶点构成网络 | 构建简单,但路径与障碍相距较近,安全性低 |
| Voronoi图法 | 由围绕障碍物的多个共边多边形组成 | 路径安全性高,但路径多在障碍之间的开阔区域,路径质量不高 |
| 栅格法 | 使用互不重叠的单元离散区域 | 不需考虑障碍情况,但数据量大,需平衡离散精度和搜索效率 |
| 概率路标图法 | 空间预设大量采样点,在此基础上搜索生成可行路径 | 复杂障碍场景中可生成 可行路径,但受采样点 设置影响大 |
| 快速随机树法 | 从起点开始,边布置 采样点边搜索路径, 直至到达终点 | 适用动态复杂障碍场 景,但受采样点生成参 数影响大,随机性高 |
| 人工势场法 | 构建虚拟力场引导 目标沿最大梯度方 向运动 | 适用复杂多障碍场景, 但势场函数设置复杂 |
2.2 多机航迹修正
2.2.1 平滑处理
平滑处理是航迹规划技术中重要组成之一, 是解决路径初规划后使路径满足无人机飞行性能约束的问题。路径初规划是由许多最短直线首尾连接而成的折线, 具有一定的角度, 而无人机受飞行性能约束, 转角有限不能都达到。研究者们对此问题提出路径修正: 轨迹曲线规划法即平滑处理, 将不满足飞行性能约束的路径, 计算修正为满足飞行约束的曲线,建立参数控制, 通过调整曲率和长度生成多样化的任务路径。常用曲线包含Dubins 曲线、贝塞尔曲线、B 样条曲线和毕达哥拉斯曲线等,对比见表2。
| 名称 | 内容 | 优缺点 |
|---|---|---|
| Dubins曲线 | 由直线和圆弧组成,可增加盘旋或调整曲率控制长度 | 计算简单且长度最短,但直线与圆弧连接处曲率不连续 |
| 贝塞尔曲线 | 由线段与节点组成,通过控制节点来调整曲线空间分布 | 曲率连续,但多段拼接困难,不能局部调整 |
| B 样条曲线 | 调整贝塞尔曲线的基函数,以分段低阶曲线代替高阶曲线 | 支持多段拼接,可局部修改,但计算复杂 |
| 毕达哥拉斯曲线 | 满足毕达哥拉斯条件 的参数化多项式曲线 | 曲率连续且长度可控,但控制参数复杂 |
除此之外,文献[41]采用CR 样条曲线是 Bezier 曲线的一种改进形式, 一种插值样条曲线, 参数方简单, 计算速度快, 具有C1连续性 (切线连续), 且修改其中某一控制点只会修改相邻的曲线变化, 不会影响距该点较远的曲线形状, 当要对某些航迹段调整时, 仅需要对部分航迹做出改变即可。 文献[42]基于Clothoid螺旋曲线的复合路径, 采用一种新的算法,与基于微分几何的迭代算法相比,能够在任意起止点位置和方向下得到更短的曲率连续的Clothoid复合路径且算法迭代简单。
2.2.2 安全距离
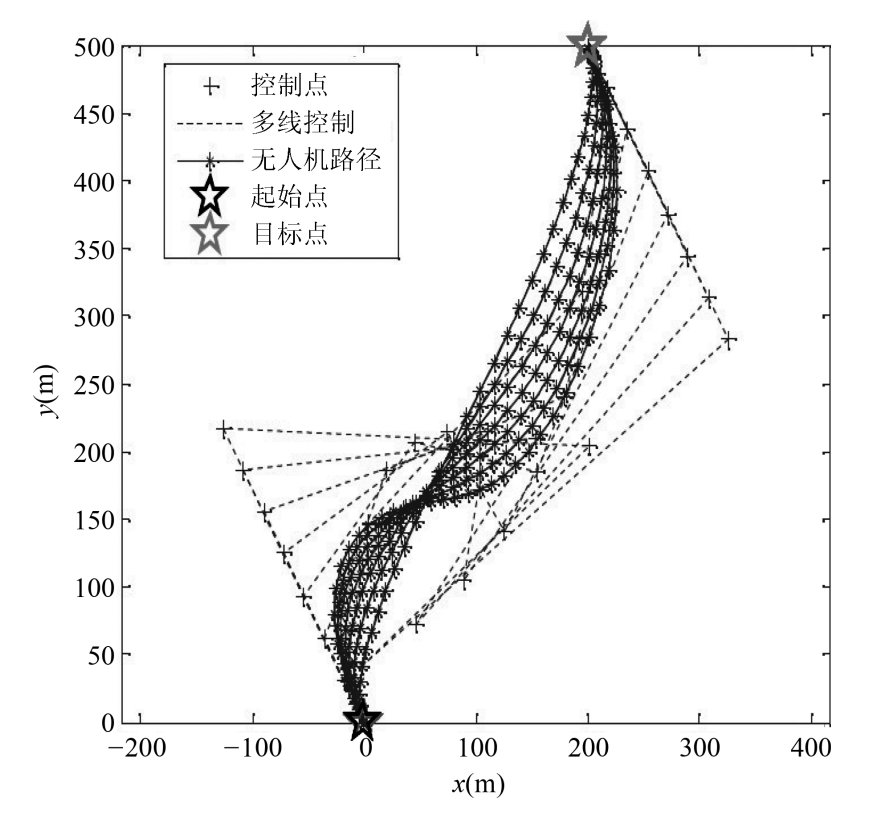
多无人机协同工作时,存在两机或多机交汇问题, 为避免无人机交汇碰撞,为无人机建立轨道安全距离, 如果不满足安全约束, 需通过改变曲率或添加中间航路点等方法, 通过 K 航迹平滑处理法、Dubins 曲线、Clothoid 螺旋曲线、PH 螺旋曲线等对路径修正, 如文献[43]仿真得到 PH 路径随切线向量长度k变化, 如图5所示[43]。文献 [44] 在城市环境和山区环境下提出使用 PH 曲线以及和声搜索算法调整飞行路径以满足空间需求, 满足无人机的运动和动态约束, 保证任何两个无人机之间都大于等于安全距离, 不存在碰撞路线以及障碍物。
此外有的研究者将躲避新障碍物问题也看作航迹安全距离问题。由于人工势场法只适用于障碍物数量不多的环境下, 文献 [45] 指出传统的人工势场仅限于单个无人机轨迹规划, 为了克服这一挑战, 提出了一种利用距离因子和跳跃策略来解决不可达目标等常见问题的方法, 并确保无人机不会碰到任何障碍物。此外, 使用动态步长调整方法解决抖动问题已在定量测试仿真模型中得到验证, 并且在模拟城市环境中获得满意的结果。
2.2.3 协调路径

3 聚类分析在任务规划中的应用
以上对多无人机任务规划有了初步全面的了解,下面以一种具体的聚类算法为例,介绍其在任务规划中的作用。
3.1 聚类算法
聚类分析将物理或抽象对象的集合分组为由类似的对象组成的多个类的分析过程。聚类分析的算法可以分为:
1) 划分法:在给定一个有 N个元组或者记录的数据集, 通过反复迭代的方法改变分组, 使得每一次改进之后的分组方案都较前一次好, 分裂法将构造K个分组, 每一个分组就代表一个聚类, 其中K < N。如: K-means 算法、K-medoids 算法、CLARANS算法等; 2) 层次法:对给定的数据集进行层次的分解, 根据聚类树的形成方式,可以分为自顶向下的分裂和自底向上的凝聚,直到某种条件满足为止。如: BIRCH 算法、CURE算法、CHAMELEO 算法等; 3) 基于密度的方法:对一个区域中的点的密度大过某个阈值, 就把它加到与之相近的聚类中去。如: DBSCAN 算法、OPTICS 算法、DENCLUE算法等; 基于网格的方法将数据空间划分成为有限个单元的网格结构所有的处理都是以单个的单元为对象。如:STING 算法、CLIQUE 算法、Wave-Cluster 算法; 4) 基于模型的方法:利用数据样本建立统计模型的无监督聚类算法。该算法通过对数据样本进行统计分析,建立适合数据分布的概率模型,然后根据数据样本与概率模型之间的符合程度进行样本划分,得到不同类别的聚类结果。如: 高斯混合模型聚类、期望最大化算法、均值漂移聚类、马尔可夫随机场聚类。
在多目标聚类常用K-means算法和 K-medoids 算法, 有效的解决了编队级目标分配问题。
3.2 K-means算法
近15 年, K 均值算法 (也称 K-means 算法) 是无人机目标聚类分析使用最多、最常用的一种动态聚类、一种基于划分的迭代算法。通过反复修改分类来达到最满意的聚类结果。其基本思想: 先以一些初始点为聚类中心, 对样本集进行初始分类, 判定分类结果是否能使一个确定的准则函数取得极值: 能, 聚类算法结束; 不能, 改变聚类中心, 重新进行分类, 并重复判定所使用的准则。设有k个分类, 每个分类域中心为mj, (j = l, 2, · · · , k ), 常用的准则函数是使得每个类中的各样本到该类中心的距离的平方和取得极小值, 为
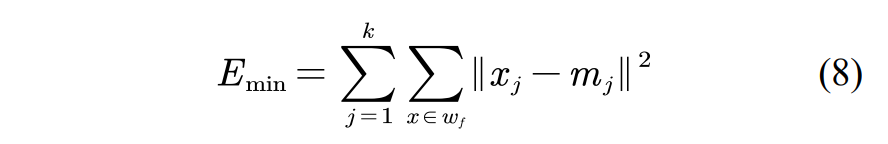
算法1. 学习率在线更新算法
1)随机选择k个样本作为初始簇类的均值向量;
2)将每个样本数据集划分离它距离最近的簇;
3)根据每个样本所属的簇,更新簇类的均值向量;
4)重复(2)(3)步,当达到设置的迭代次数或簇类的均值向量不再改变时,模型构建完成,输出聚类算法结果。
该算法的优点是原理简单,实现容易,且时间复杂度不高,为O(iter x N x k x d),其中iter为迭代次数,N为数据点数量,k为簇的数量,d为数据点维数,时间复杂度与样本数量线性相关,对于处理大数据集合十分高效,且伸缩性较好。
该算法的缺点是:1)聚类中心的个数k需要事先给定,但在实际中该值的选定是难以估计的;2)需要人为地确定初始聚类中心,不同的初始聚类中心可能导致完全不同的聚类结果,即对初始值敏感;3)结果不一定是全局最优,只能保证局部最优;4)对噪声和离群点敏感;5)不适于发现非凸面形状的簇或大小差别很大的簇;6)需样本存在均值,限定了数据种类。这也为后续对K-means的改进提供思路。
3.3 任务目标分配
针对任务类型相似而目标对象有多个时,也需要进行任务/目标的分配,利用聚类方法将距离相近的目标聚成一类派出同一架无人机,可以缩小无人机移动的范围。而上述K-means算法的k值确定是一个难点,则可以根据无人机的数量确定k值,或者根据簇群数量反向确定无人机数量进行任务分配,通过K-means这样确定中心点建立目标簇完成编队级目标分配, 就可将最近的目标簇分配给该无人机编队, 如图6,简化了多无人机——多目标分配问题[50], 从整体上提高了目标分配求解效率。
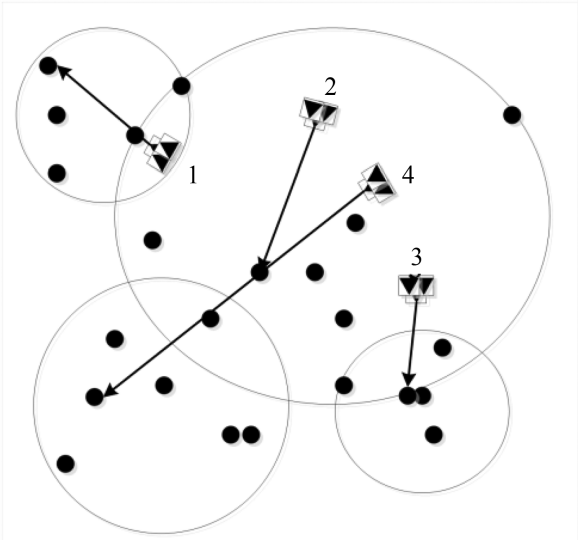
但是, 传统 K-means聚类算法对初始值、异常值很敏感,不适用于非凸形状的数据分布。许多研究者以改变初始聚点或修改聚点等对传统K均值聚类算法进行改进, 如: K-means 改进的 K-medoids 算法[45], K-means 是以当前 Cluster 中所有数据点的平均值为中心点, 而 K-medoids 以当前Cluster 内满足到其他所有点的距离之和最小的样本点为中心点; 此外文献 [46]是以所有数据成员到聚类中心的距离与聚类的半径阈值对比判定中心点的办法改进传统 K 均值方法, 当出现距离大于设定的聚类的半径阈值时, 该点为新的中心点。再依次检测所有数据成员到聚类中心的距离是否小于等于聚类的半径阈值, 若都小于等于则该点为聚类中心。以60个目标仿真后得到改进后K均值方法在求解预攻击目标聚类问题时,在误差平方和准则函数、样本数量均匀、类间距离和类内距离之比方面均优于传统K均值方法, 但计算量增大且计算的时间相对变长。
3.4 多航迹规划
聚类分析法还可用于多航迹规划, 多航迹规划利用先聚类后规划的思想,能够在突发威胁多发区域生成多条备选路线,提高无人机应对突发危险的能力。
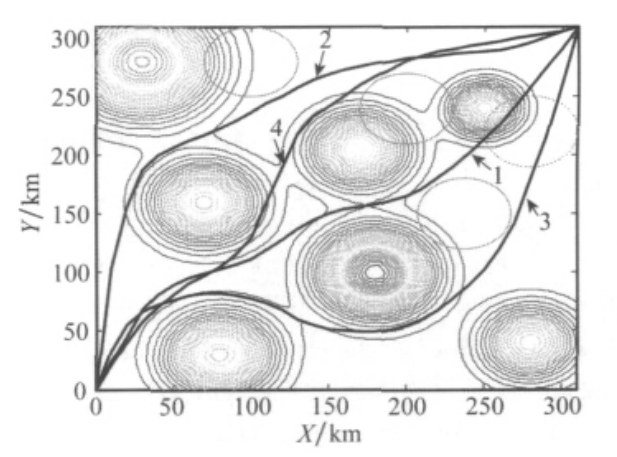
文献[47]提出了将粒子群优化(particle swarm optimization, PSO)算法与加权K均值聚类算法相结合的规划方法。每个粒子表示一条航迹,采用加权K 均值聚类算法对粒子进行分类,得到多个粒子子群,在每个子群内部进行一条可行航迹的优化,最终得到多条不同的可行航迹。针对K均值聚类算法对初始值敏感的问题,文献对此进行改进,采用排挤机制产生初始聚类中心;针对实际环境中突发威胁的分布不均性,在聚类过程中,对航迹节点按照所在区域突发威胁的出现概率进行加权,提出了加权K 均值聚类算法。仿真实验表明,所提出的方法能够有效地得到无人机的多条可行航迹,如图7所示,K=4时生成4条航线,其中航迹1和4的初始路径相似,在中后半段有所不同,在全局静态条件下,航线1具有最小的代价是最优的,但航线1前方有突发威胁时,只要及时发现危险,则能够有效地从最优航迹1切换到航迹4。若没有进行多航迹规划或利用加权K均值算法,则无法应对这种突发情况。
文献[48]为了高效地规划无人机在三维覆盖检测任务的飞行路径,建立了满足覆盖率要求的路径规划模型,可分为两步:1.确定无人机巡检的视点和视线;2.计算视点的无碰撞访问序列。首先,从巡检目标的三维点云出发,提出基于K均值聚类生成候选视点的方法,构建候选视点互连的非完全图模型;其次,提出面向排序的混合蚁群算法(sorting-oriented hybrid ant colony algorithm, S-HACO)求取无人机巡检路径,优化目标考虑了路径长度、视点数目、急转弯次数等。经仿真,该方法得到的视点数目减少、性能更优、运行时间更短。
4 结 论
多无人机协同是无人机向智能化发展的必然趋势,任务规划则是确保任务高效有序完成的必由之路。其一,任务分配方面,涉及任务类型与无人机载荷的相互匹配,抽象成带约束条件的组合优化问题,可由多种算法求解,包括静态、动态、集中式和分布式,各有特点和适用范围。其二,路径规划方面,单路径规划的算法发展成熟且多样化,关键在于涉及多架无人机时的航迹修正,保证安全距离和任务时序约束。前两章的综述重在对整体的把握,为更深入了解任务规划,第三章选取具体的K均值聚类算法,介绍其改进算法实现多无人机-多目标分配和多航迹规划。未来,该方向发展潜力巨大,如建立有效的任务规划效能评估机制、在现有算法基础上创新以提高任务规划的效率、考虑不确定因素对建模的影响提高模型的实用性和鲁棒性等。希望本文的研究对于全面了解多无人机任务规划研究现状和关键技术具有良好的参考意义。
参 考 文 献
[1] 赵林,张宇飞,姚明旿,等. 无人机集群协同技术发展与展望[J] . 无线电工程,2021,51(8) :823- 828.
ZHAO Lin, ZHANG Yufei, YAO Mingwu, et al. Development and Trend of UAV Swarm Cooperative Techniques[J].Radio Engineering,2021,51(8):823-828.
[2] XIE J, CARRILLO L R G, JIN L. An Integrated Traveling Salesman and Coverage Path Planning Problem for Unmanned Aircraft Systems[J]. IEEE Control Systems Letters,2019, 3(1): 67-72.
[3] WANG Z, LIU L, LONG T, et al. Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double-chromosome encoding[J]. Chinese Journal of Aeronautics, 2017, 31(2): 339-350.
[4] YE F, CHEN J, TIAN Y, et al. Cooperative Multiple Task Assignment of Heterogeneous UAVs Using a Modified Genetic Algorithm with Multi-type-gene Chromosome Encoding Strategy[J]. Journal of Intelligent & Robotic Systems, 2020, 100(2): 615-627.
[5] WU W, CUI N. A distributed and integrated method for cooperative mission planning of multiple heterogeneous UAVs[J]. Aircraft Engineering and Aerospace Technology, 2018, 90(9): 1403-1412.
[6] DENG Q, YU J, MEI Y. Deadlock-Free Consecutive Task Assignment of Multiple Heterogeneous Unmanned Aerial Vehicles[J]. Journal of Aircraft, 2014, 51(2): 596-605.
[7] FU X, FENG P, GAO X. Swarm UAVs Task and Resource Dynamic Assignment Algorithm Based on Task Sequence Mechanism[J]. IEEE Access, 2019, 7: 41090-41100.
[8] FU X, FENG P, LI B, et al. A Two-Layer Task Assignment Algorithm for UAV Swarm Based on Feature Weight Clustering[J]. International Journal of Aerospace Engineering, 2019, 2019:3504248.
[9] XU G, LONG T, WANG Z, et al.Target-bundled genetic algorithm for multi-unmanned aerial vehicle cooperative task assignment considering precedence constraints[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 234(3): 760 -773.
[10] KOPEIKIN A N, PONDA S S, JOHNSON L B, et al. Real-time dynamic planning to maintain network connectivity in a team of unmanned air vehicles[C]. IEEE GLOBECOM Workshops (GC Wkshps), 2011: 1303-1307.
[11] LIU J, LIAO X, YE H, et al. UAV Swarm Scheduling Method for Remote Sensing Observations during Emergency Scenarios[J]. Remote Sensing, 2022, 14(6): 1406.
[12] 齐乃明,孙小雷,董程等.航迹预测的多无人机任务规划方法[J].哈尔滨工业大学学报,2016,(4):32-36.
QI Naiming, SUN Xiaolei, DONG Cheng, et al. Journal of Harbin Institute of Technology, 2016, (4): 32-36.
[13] KURDI H, HOW J, BAUTISTA G. Bio-Inspired Algorithm for Task Allocation in Multi-UAV Search and Rescue Missions[C]. AIAA Guidance, Navigation, and Control Conference, 2016: 2283-2291.
[14] BUCKMAN N, HOW J P, CHOI H-L. Partial Replanning for Decentralized Dynamic Task Allocation[C]. AIAA Scitech Forum, 2019: 1174-1184.
[15] OH G, KIM Y, AHN J, et al. Market-Based Task Assignment for Cooperative Timing Missions in Dynamic Environments[J]. Journal of Intelligent & Robotic Systems, 2017, 87(1): 97-123
[16] MERCKER T, CASBEER D W, MILLET P T, et al. An extension of consensus-based auction algorithms for decentralized, time-constrained task assignment[C]. American Control Conference, 2010: 6324-6329.
[17] KOPEIKIN A N, PONDA S S, JOHNSON L B, et al. Dynamic Mission Planning for Communication Control in Multiple Unmanned Aircraft Teams[J]. Unmanned Systems, 2013, 1(1): 41-58.
[18] WHITTEN A K, CHOI H-L, JOHNSON L B, et al. Decentralized task allocation with coupled constraints in complex missions[C]. American Control Conference, 2011:1642-1649.
[19] NUNES E, MANNER M, MITICHE H, et al. A taxonomy for task allocation problems with temporal and ordering constraints[J]. Robotics and Autonomous Systems, 2017, 90: 55-70.
[20] DENG Q, YU J, MEI Y. Deadlock-Free Consecutive Task Assignment of Multiple Heterogeneous Unmanned Aerial Vehicles[J]. Journal of Aircraft, 2014, 51(2): 596-605.
[21] CHEN Y, YANG D, YU J. Multi-UAV Task Assignment With Parameter and Time-Sensitive Uncertainties Using Modified Two-Part Wolf Pack Search Algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(6): 2853-2872.
[22] XU G, LONG T, WANG Z, et al. Target-bundled genetic algorithm for multi-unmanned aerial vehicle cooperative task assignment considering precedence constraints[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 234(3): 760 -773.
[23] CASBEER D, HOLSAPPLE R. Column generation for a UAV assignment problem with precedence constraints[J]. International Journal of Robust and Nonlinear Control, 2011, 21: 1421-1433.
[24] WANG Y, RU Z Y, WANG K, et al. Joint Deployment and Task Scheduling Optimization for Large-Scale Mobile Users in Multi-UAV-Enabled Mobile Edge Computing[J]. IEEE Trans Cybern, 2020, 50(9): 3984-3997.
[25] HU C, LU J, LIU X, et al. Robust vehicle routing problem with hard time windows under demand and travel time uncertainty[J]. Computers & Operations Research, 2018, 94: 139-153.
[26] XIA C, LIU Y, YIN L, et al. Cooperative Task Assignment and Track Planning For Multi-UAV Attack Mobile Targets[J]. Journal of Intelligent & Robotic Systems, 2020, 100(3): 1383-1400.
[27] CHEN H, NAN Y, YANG Y. Multi-UAV Reconnaissance Task Assignment for Heterogeneous Targets Based on Modified Symbiotic Organisms Search Algorithm[J]. Sensors, 2019, 19(3): 734.
[28] LIU H, LI X, WU G, et al. An Iterative Two-Phase Optimization Method Based on Divide and Conquer Framework for Integrated Scheduling of Multiple UAVs[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(9): 5926-5938.
[29] ATENCIA C R, SER J D, CAMACHO D. Weighted strategies to guide a multi-objective evolutionary algorithm for multi-UAV mission planning[J]. Swarm and Evolutionary Computation, 2018, 44: 480-495.
[30] YAO W, QI N, WAN N, et al. An iterative strategy for task assignment and path planning of distributed multiple unmanned aerial vehicles[J]. Aerospace Science and Technology, 2019, 86: 455-464.
[31] CHOI H L, BRUNET L, HOW J P. Consensus-Based Decentralized Auctions for Robust Task Allocation[J]. IEEE Transactions on Robotics, 2009, 25(4): 912-926.
[32] 严飞, 祝小平, 周洲, 等. 考虑同时攻击约束的多异构无人机实时任务分配[J]. 中国科学:信息科学, 2019, 49(5): 555-569.
YAN F, ZHU X P, ZHOU Z, et al. Real-time task allocation for a heterogeneous multi-UAV simultaneous attack[J]. Sci Sin Inform, 2019, 49(5): 555-569.
[33] YE F, CHEN J, SUN Q, et al. Decentralized task allocation for heterogeneous multi-UAV system with task coupling constraints[J]. The Journal of Supercomputing, 2021, 77(1): 111-132.
[34] HU X, LIU Y, WANG G. Optimal search for moving targets with sensing capabilities using multiple UAVs[J]. Journal of Systems Engineering and Electronics, 2017, 28(3):526-535.
[35] 王琼,刘美万,任伟建等.无人机航迹规划常用算法综述[J].吉林大学学报:信息科学版,2019,(1): 58-67.
Wang Qiong, Liu Meiwan, Ren Weijian, et al. Journal of Jilin University : Information Science, 2019,(1): 58-67.
[36] WOLEK A, CHENG S, GOSWAMI D, et al. Cooperative Mapping and Target Search Over an Unknown Occupancy Graph Using Mutual Information[J]. IEEE Robotics and Automation Letters, 2020, 5: 1071-1078.
[37] ZHEN Z, ZHU P, XUE Y, et al. Distributed intelligent self-organized mission planning of multi-UAV for dynamic targets cooperative search-attack[J]. Chinese Journal of Aeronautics, 2019, 32(12): 2706-2716.
[38] ZHEN Z, GAO C, ZHENG F, et al. Cooperative path replanning method for multiple unmanned aerial vehicles with obstacle collision avoidance under timing constraints[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(10): 1813-1823.
[39] HU J, WANG M, ZHAO C, et al. Formation control and collision avoidance for multi-UAV systems based on Voronoi partition[J]. Science China Technological Sciences, 2019, 63(1): 65-72.
[40] FU Z, MAO Y, HE D, et al. Secure Multi-UAV Collaborative Task Allocation[J]. IEEE Access, 2019, 7: 35579-35587.
[41] CUI J, WEI R, LIU Z, et al. UAV Motion Strategies in Uncertain Dynamic Environments: A Path Planning Method Based on Q-Learning Strategy[J]. Applied Sciences, 2018, 8(11): 2169.
[42] 张安, 杨咪, 毕文豪, 等. 基于多策略 GWO算法的不确定环境下异构多无人机任务分配[J]. 航空学报, 2022, 44: 327115.
ZHANG A, YANG M, BI W H, et al. Task allocation of heterogeneous multi-UAV in uncertain environment based on multiple strategies GWO[J]. Acta Aeronautica et Astronautica Sinica, 2022, 44: 327115.
[43] YANG Xiuxia, ZHOU Weiwei, ZHANG Yi. On Collaborative Path Planning for Multiple UAVs Based on Pythagorean Hodograph Curve[C].//Proceedings of 2016 IEEE Chinese Guidance, Navigation and Control Conference (IEEE CGNCC2016).2016:1187-1191.
[44] WU J Y, GAO J-Y-L ,LI X Y. Cooperative path planning of multiple UAVs based on PH curves and harmony search algorithm[C]//Computer Supported Cooperative Work in Design (CSCWD), 2017 IEEE 21st International Conference on, 2017: 540−544.
[45] 叶青松,胡笑旋,马华伟.多无人机编队协同目标分配的两阶段求解方法[J].合肥工业大学学报:自然科学版,2015,(10):1431-1436..
YE Qingsong, HU Xiaoxuan, MA Huawei. Two-stage solution method for multi-UAV formation collaborative target allocation[J].Journal of Hefei University of Technology: Natural Science Edition,2015,(10):1431-1436.
[46] 赵敏.分布式多类型无人机协同任务分配研究及仿真[D].南京理工大学,2009.
ZHAO Min. Research and simulation of distributed multi-type UAV collaborative task allocation[D]. Nanjing University of Science and Technology, 2009.
[47] 李猛,王道波,盛守照等.基于加权k-均值聚类与粒子群优化的多航迹规划[J].系统工程与电子技术,2012,(3):512-516.
LI Meng, WANG Daobo, SHENG Shouzhao, et al. Multi-track programming based on weighted k-means clustering and particle swarm optimization[J].Systems Engineering and Electronics,2012,(3):512-516.
[48] 陈丽,陈洋,杨艳华.面向三维结构视觉检测的无人机覆盖路径规划[J].电子测量与仪器学报,2023,(2):1-10.
CHEN Li, CHEN Yang, YANG Yanhua. Unmanned aerial vehicle (UAV) coverage path planning for three-dimensional structural visual inspection[J]. Journal of Electronic Measurement and Instrumentation, 2023,(2):1-10.
[49] 王建峰,贾高伟,郭正等.多无人机协同任务规划方法研究综述[J].系统工程与电子技术,2023.
WANG Jianfeng, JIA Gaowei, GUO Zheng, et al. A review of collaborative mission planning methods for multi-UAV[J]. Systems Engineering and Electronic Technology,2023.
[50] 杨晨,张少卿,孟光磊.多无人机协同任务规划研究[J].指挥与控制学报,2018,(3):234-248.
YANG Chen, ZHANG Shaoqing, MENG Guanglei. Journal of Command and Control, 2018,(3):234-248.




