一、 设计内容及指标要求
弹簧小车根据机理法建模,先受力分析得到系统动力学微分方程,然后进行拉氏变换得到系统传递函数。
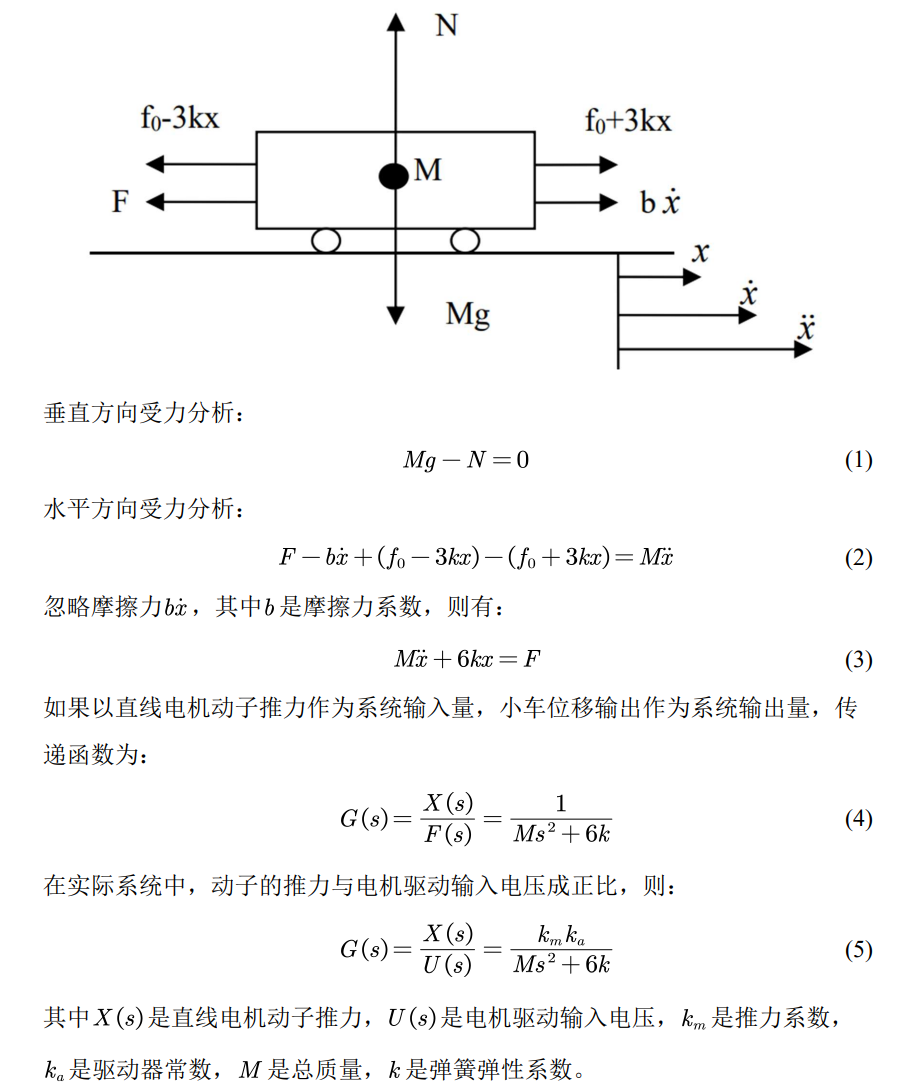
某弹簧小车系统经过模型辨识后,得到的系统模型(系统开环传递函数)为:

二、 待校正系统分析及设计方案
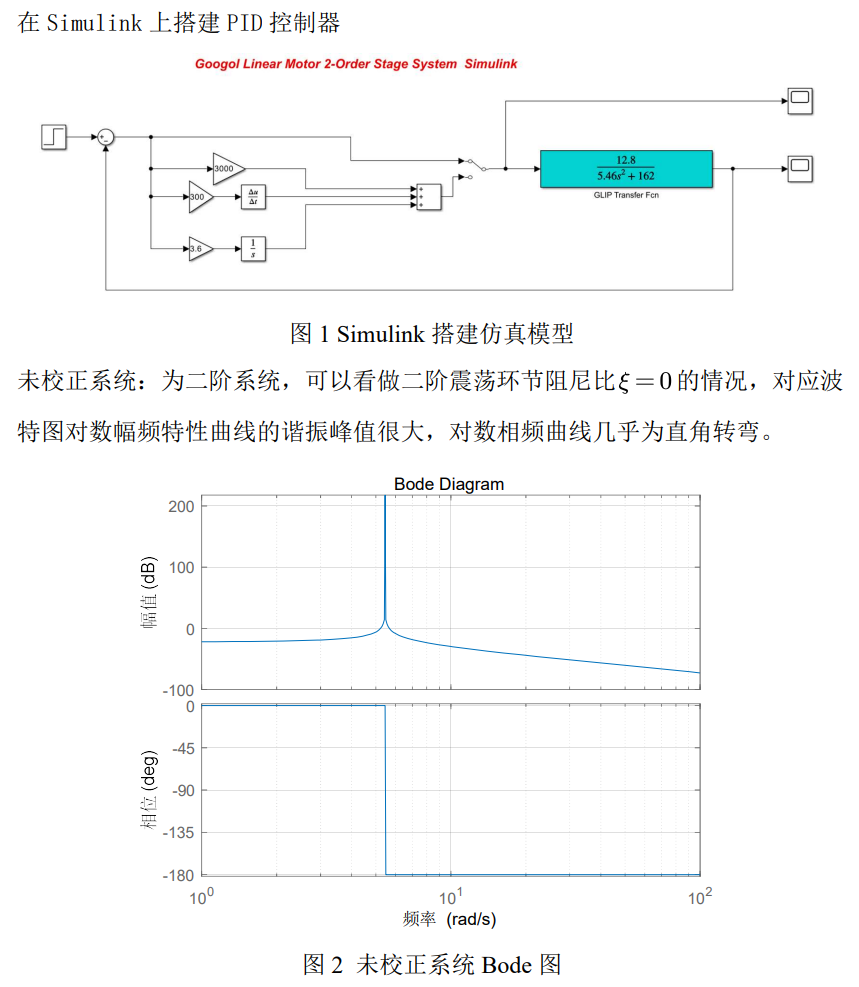
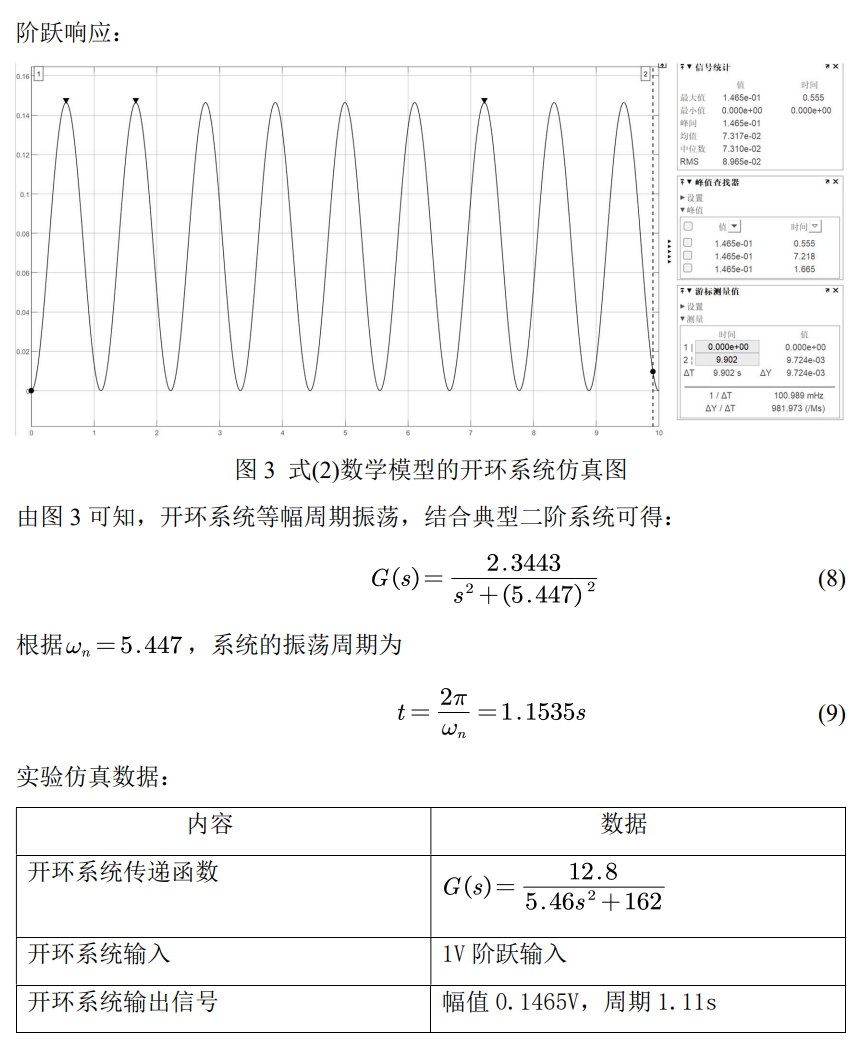
加上矫正系统之后,原系统将变成三阶或三阶以上的高阶系统,要准确推导出开环频域特征量与时域指标 超调量和调节时间之间的关系是较困难的,可以利用近似公式或者读图。计算出相角裕度,后画出波特图设计PID参数进行校正。
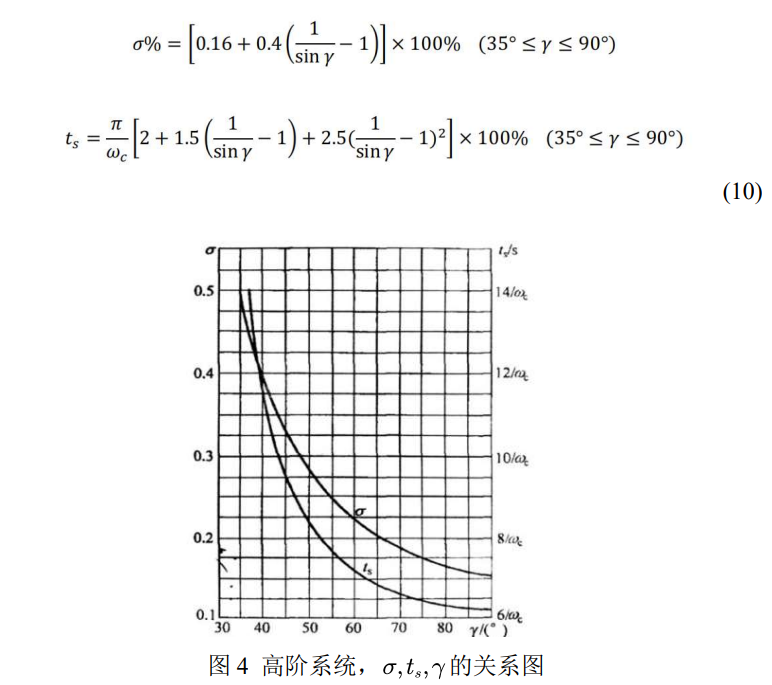
按照上述计算,高阶系统的超调量不可能小于0.1,与题设矛盾,但使用matlab仿真可以实现,这可能是由于该公式为近似公式且需要满足一定相角裕度才能使用。故选用其他设计方案将在第三节介绍。
三、 控制器设计方法与设计步骤
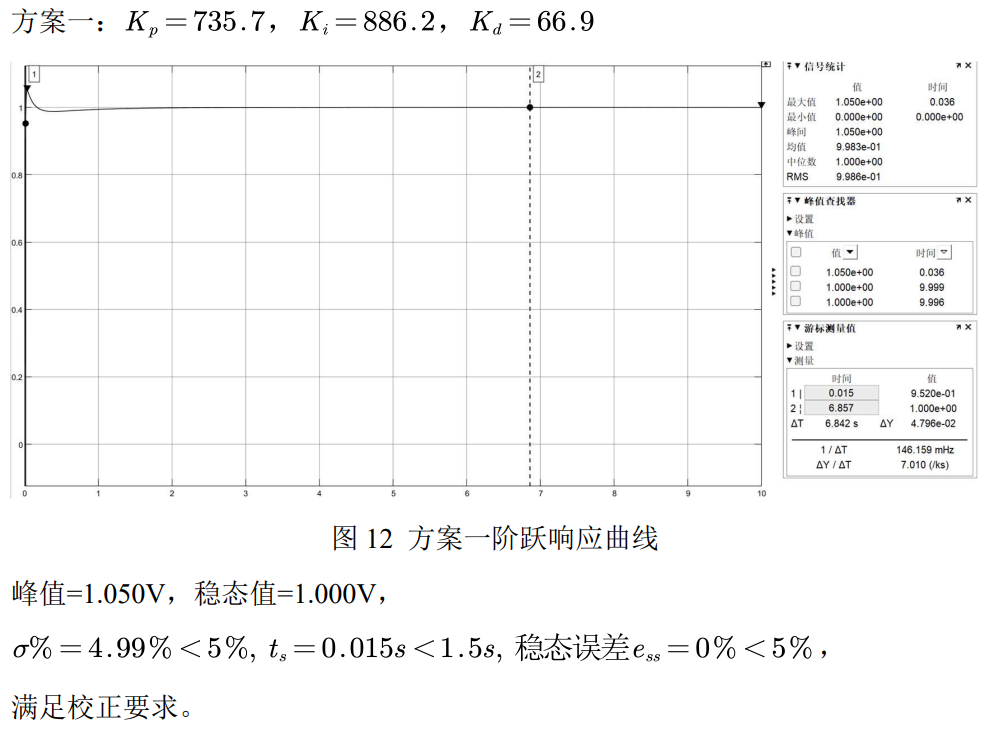
方案一:使用PID controller的自动调节,调节Response Time和Transient Behavior至要求范围内,读取参数。
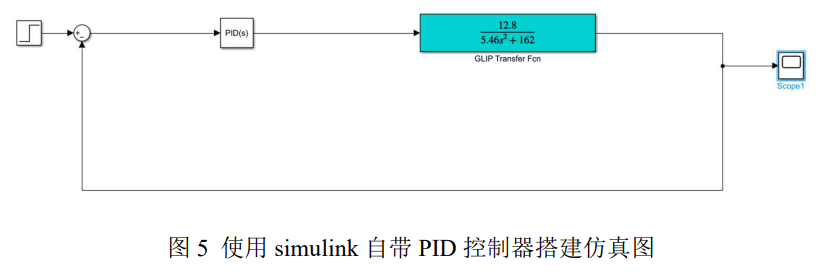
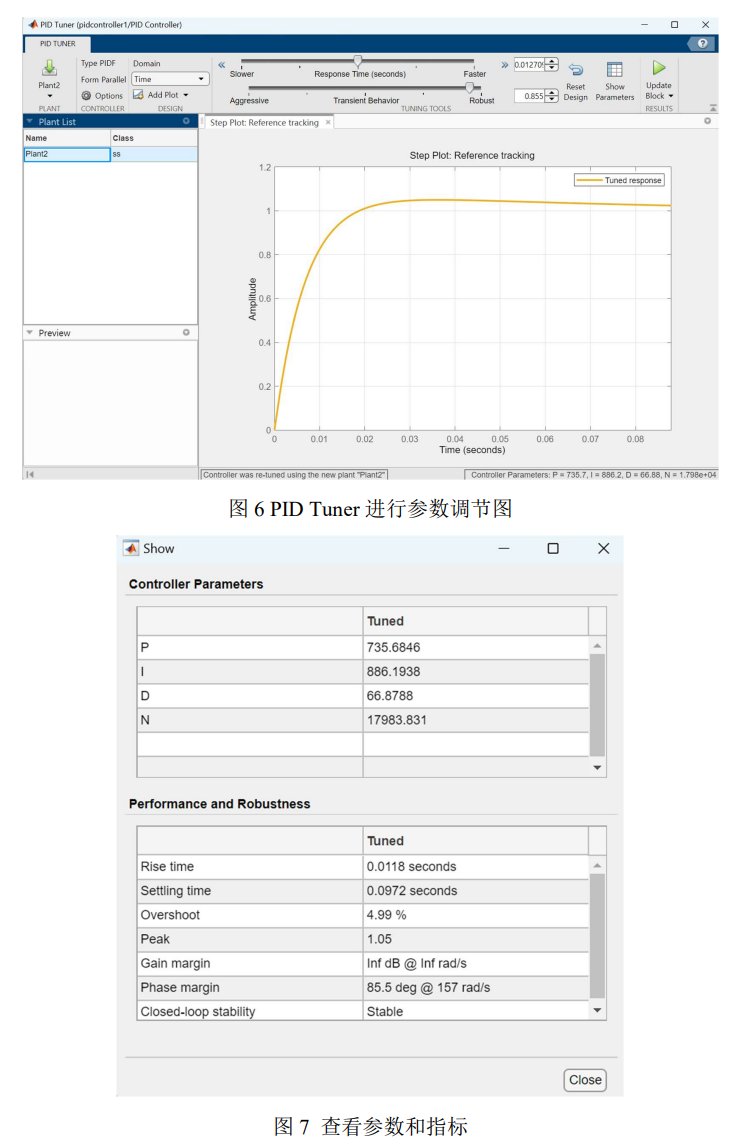
在Kp=735.7,Ki=886.2,Kd=66.9的参数下,系统调节时间为0.0972s,超调量为4.99%。
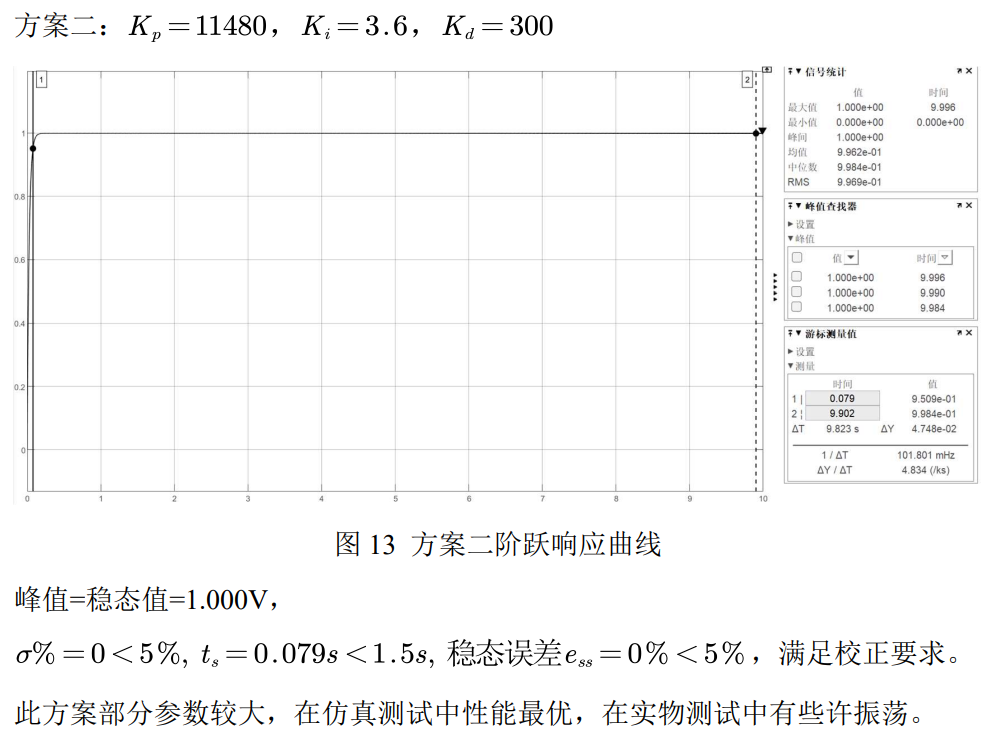
方案二:通过比例-微分-积分搭建一个PID控制器,了解PID三个参数对应的实际意义后进行调整,校正后系统:
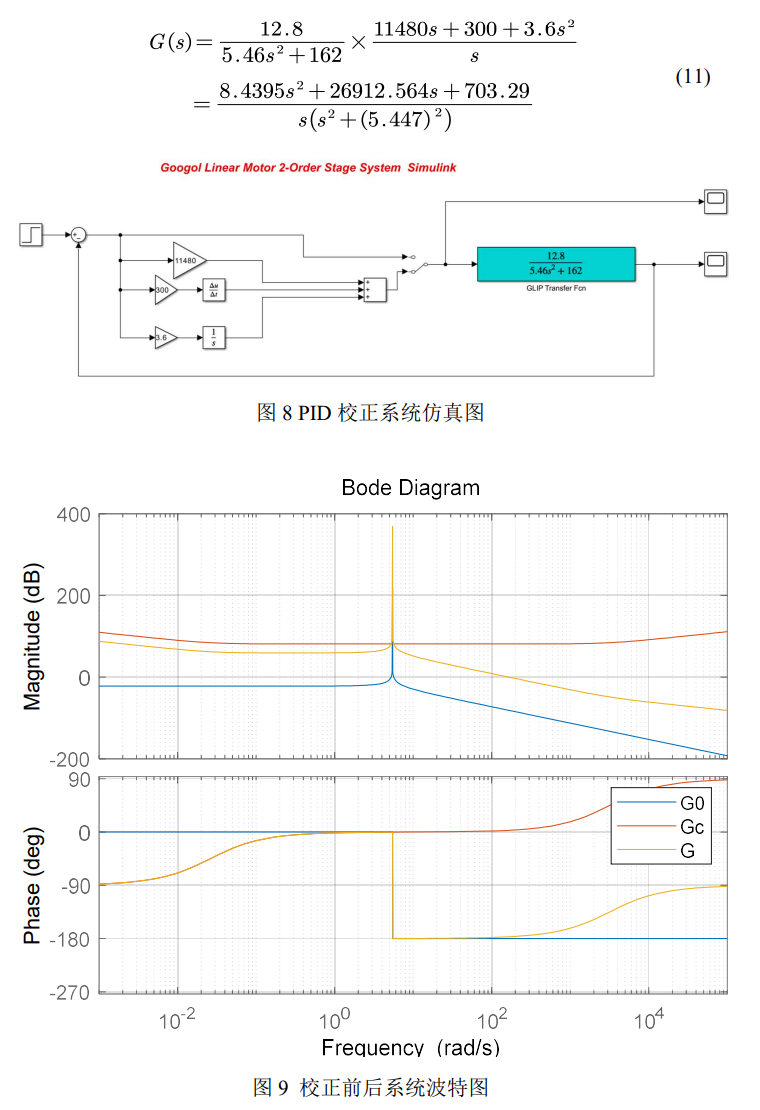
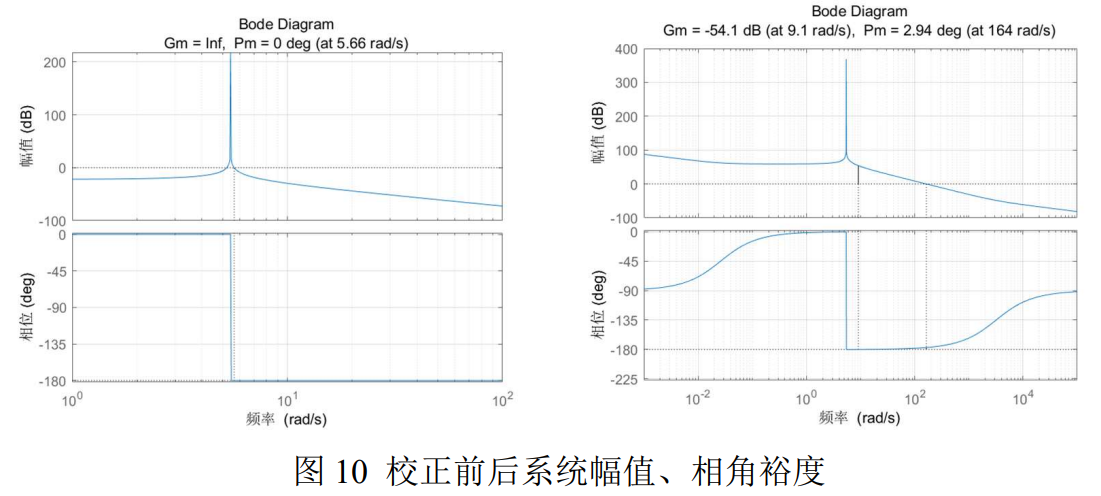
可见,幅值裕度从无穷提升到了54.1dB,相角裕度从0提升到2.94°。
方案三:试求出三个参数的比例关系,再调整实际数值,将传递函数写成如下形式:
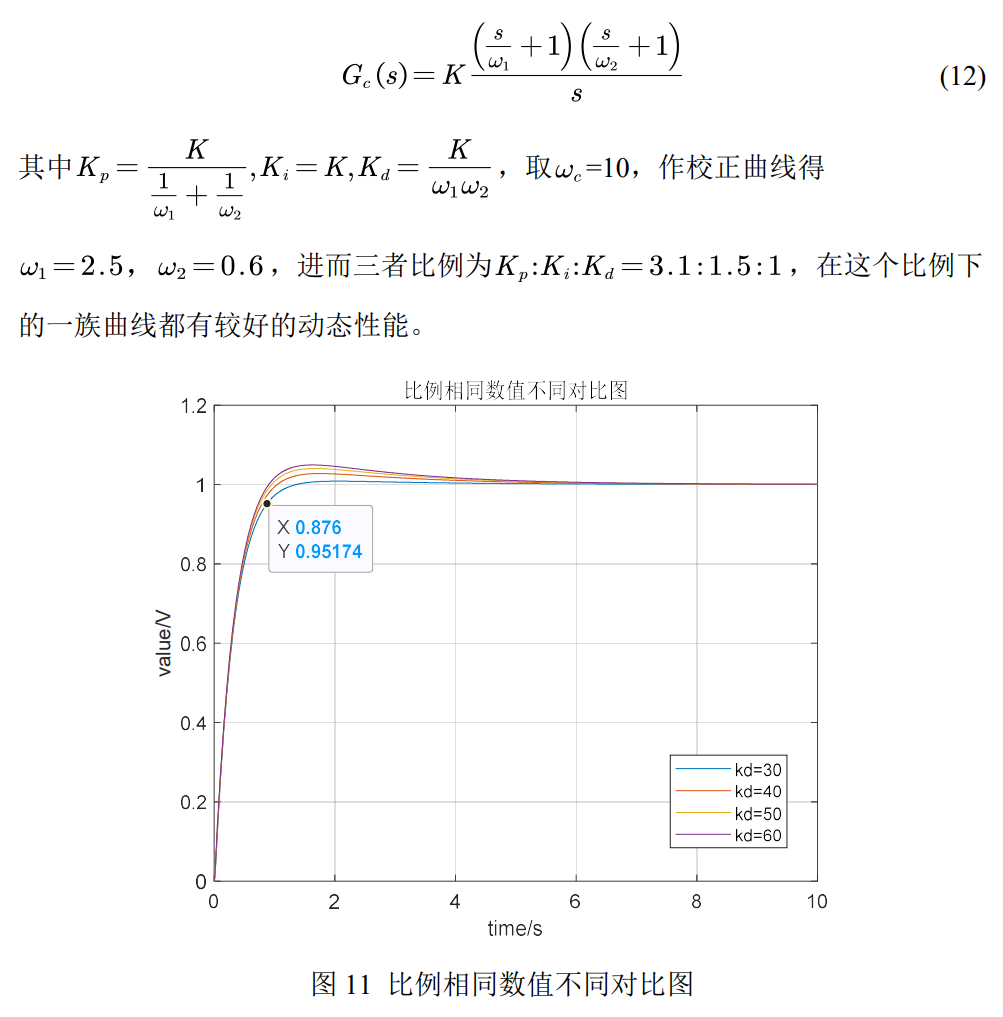
四、 仿真或分析
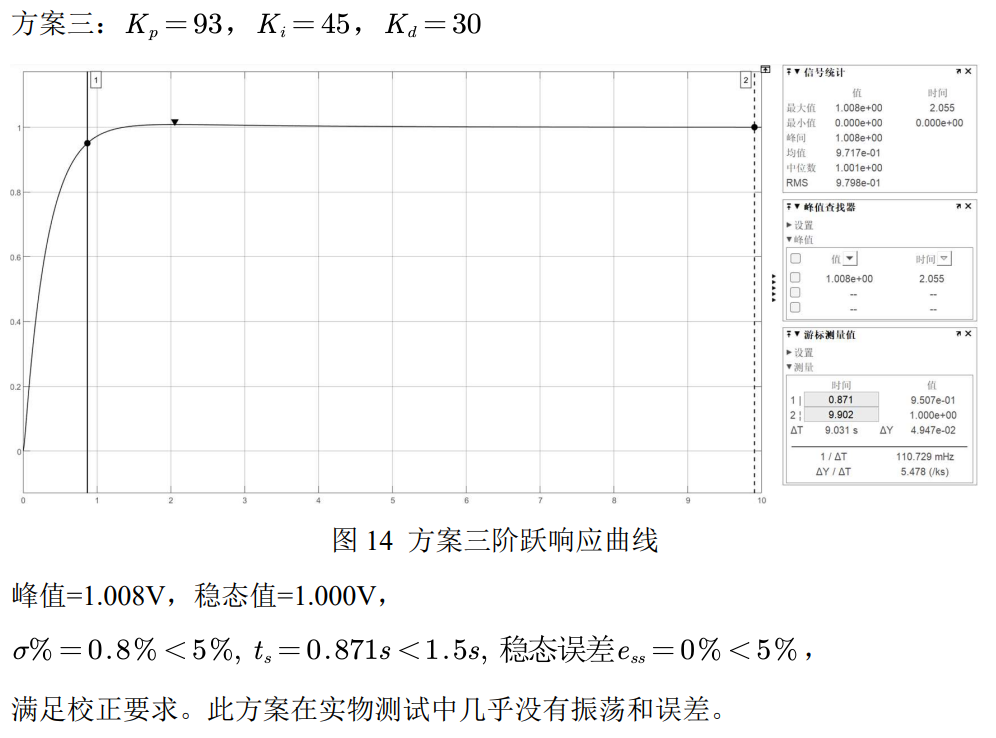
五、 实验结果
1、使用三种方法完成了PID校正装置的设计,使其满足要求的性能指标。
2、改变PID参数,观测并记录它们对控制系统的性能影响。
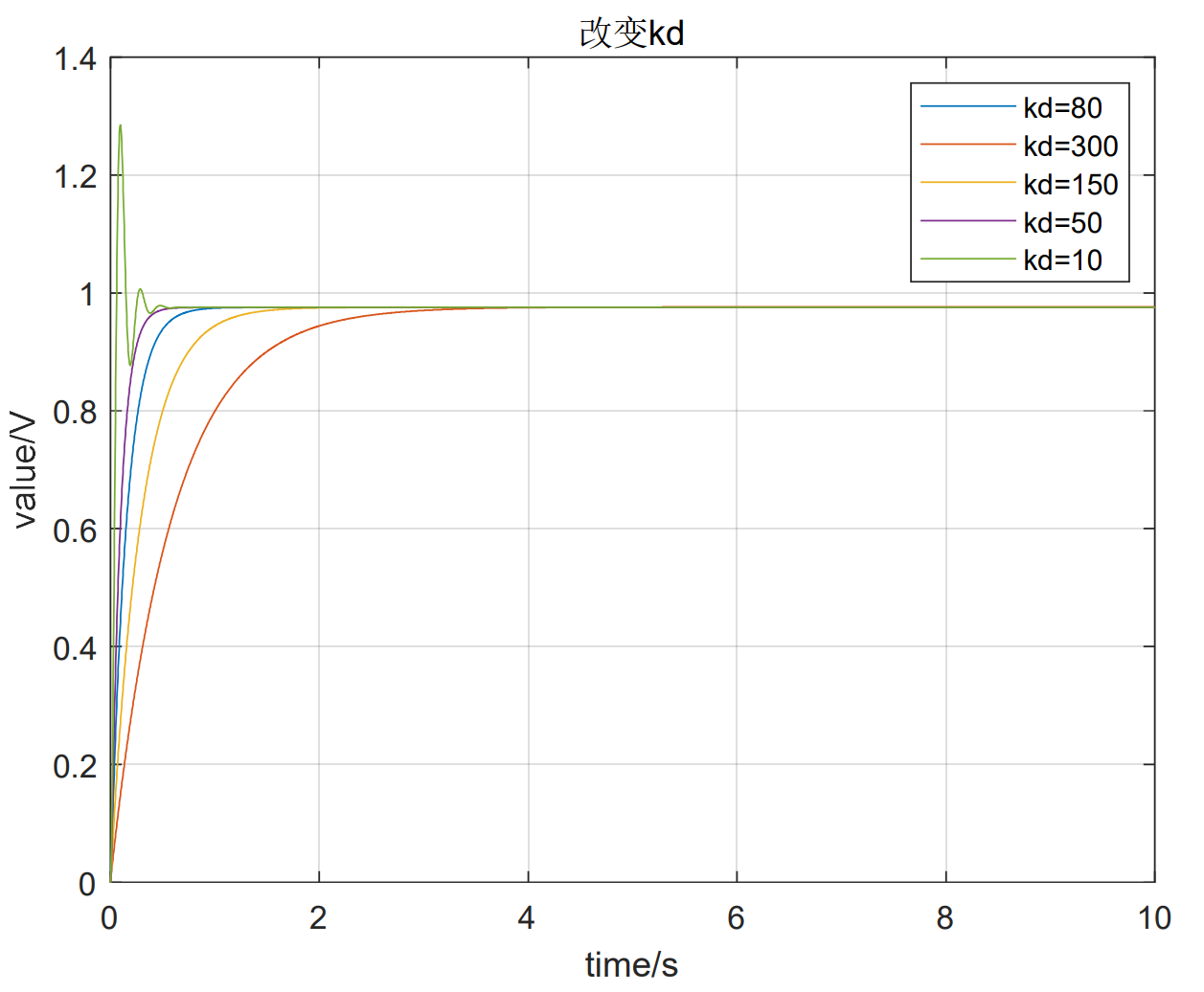
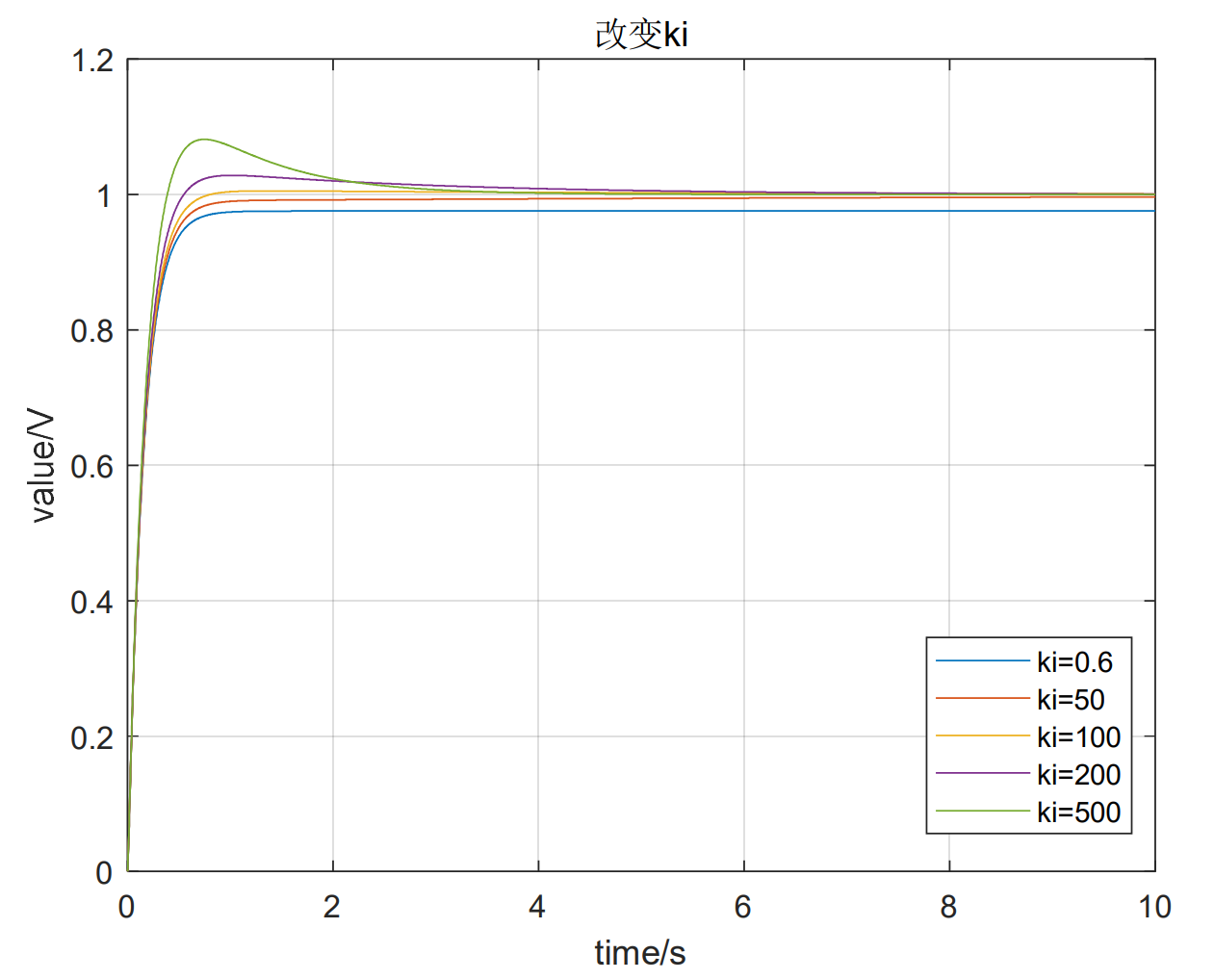
取初始参数Kp=500,Ki=0.6,Kd=80,阶跃响应曲线如下,为蓝色:
| 改变Kp,Kp越大稳态误差越小,调节时间越短,增加到一定值时,超调量增加,Kp减小则相反。 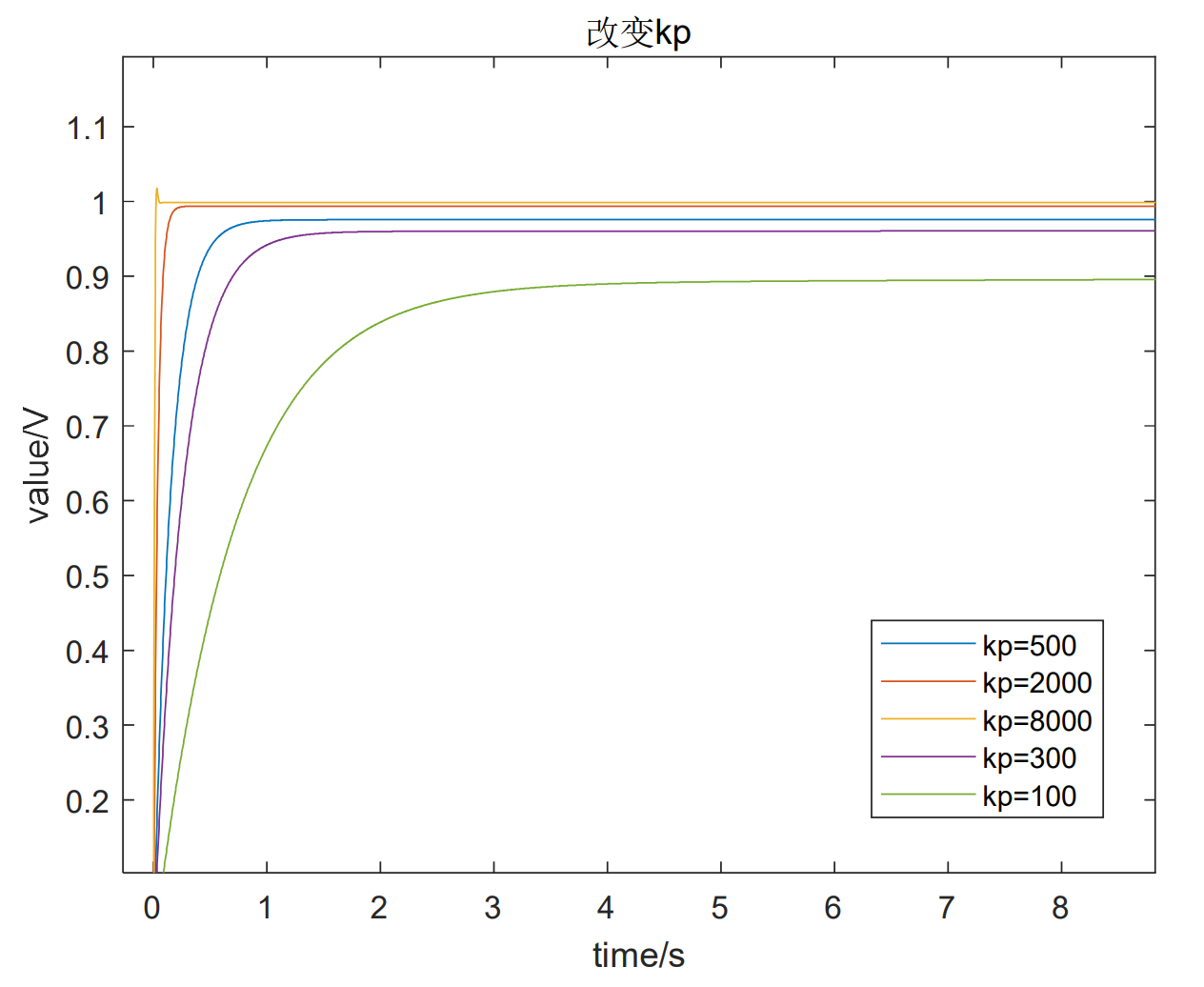
六、结论
1、弹簧小车的仿真模型是在理想情况下建立的,实际环境中的指标则会有一些误差,比如小车的磨损生锈会影响到摩擦力重量等等,仿真出响应曲线最优者在实物上不一定是效果最好,可能是由于模型偏差。
2、从宏观角度来说,PID比例-积分-微分三个参数分别对应现在、过去和未来,要根据系统的性质来判断如何调参。从实际角度来说,通过对三个参数的改变并观察输出,可知比例环节可以加快系统响应速度和精度,但有可能会增加超调和振荡,积分环节可以减小误差,但调节时间会增大,微分环节相当于加入了阻尼,可以使振荡快速衰减,变得稳定。三个参数和时域指标关系如下表,三个参数之间和每个参数和三个指标之间都有一定相互制约关系,为调参提供了依据。
| 增大 | 超调量 | 调节时间 | 稳态误差 |
|---|---|---|---|
| Kp | 增大 | 减小 | 减小 |
| Ki | 增大 | 增大 | 减小 |
| Kd | 减小 | 增大 | 不变 |
3、PID抗干扰性好,而且结构简单,无论用程序还是电路搭建都比较容易,系统反应明确,每次运行一致性好;有各种改进方法可选,还有各种配套的环节和控制结构。综上所述,因此工业中PID控制有广泛的应用。
4、有积分特性的控制器普遍存在积分饱和问题,这种控制器只要偏差没有消失,其输出就会按偏差的极性向两个极端位置(最大或最小)的方向变化。避免输出饱和,可以采用限幅装置。