AdaBoost算法原理推导与实验

1 AdaBoost算法简介

1.1 背景与意义

在当今大数据时代，数据挖掘成为从海量数据中提取有价值信息的关键技术之一。随着数据量的不断增加，传统的机器学习算法在应对复杂问题时逐渐显露出一些不足。因此，强大而高效的算法成为研究和实践的焦点之一。AdaBoost(Adaptive Boosting)算法就是在这个背景下应运而生的一种集成学习算法。

本文旨在深入探讨AdaBoost算法的提出背景、发展应用、原理推导，通过对其算法仿真以及迭代过程的研究，对数据挖掘领域有进一步的认识。AdaBoost是一种集成学习方法，它通过组合多个弱学习器来构建一个强大的分类器，具有在实际问题中取得出色性能的潜力。它的自适应在于：前一个弱分类器分错的样本的权值会得到加强，权值更新后的样本再次被用来训练下一个新的弱分类器。在每轮训练中，用样本总体训练新的弱分类器，产生新的样本权值，一直迭代直到达到预定的错误率或达到指定的最大迭代次数。通过深入研究该算法，我们可以更好地理解其工作原理，为实际问题选择合适的参数配置，进而在实际应用中取得更好的性能。

1.2 起源与发展

AdaBoost是一种著名的集成学习算法，最初由Yoav Freund和Robert Schapire于1996年提出。在提出AdaBoost之前，机器学习领域存在一个问题，即如何将多个弱分类器（比如简单的决策树或单层神经网络）组合成一个强大的分类器。传统的方法是均匀地组合多个弱分类器的决策，但这并不总行之有效。AdaBoost提出了一种新的集成学习方法，它通过动态调整样本的权重，让那些先前分类错误的样本在后续学习中得到更多的关注。

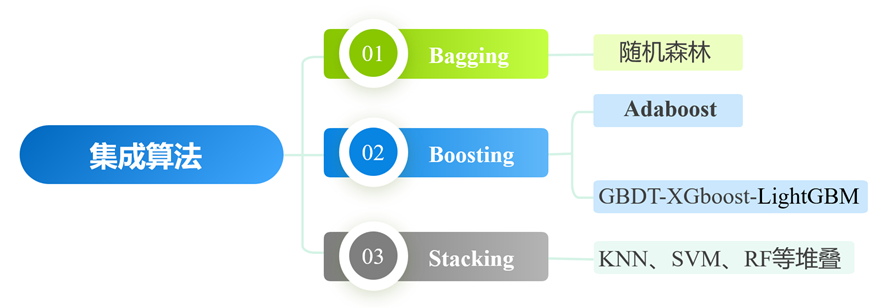
AdaBoost是集成学习(Ensemble Learning)的一个分支，运用多个模型（又称学习器）共同解决问题，集成学习能让机器学习效果更好，泛化性能更强，对于解决复杂问题非常有效。集成学习的思想是一个强学习器对算力和服务器性能的要求很高，训练代价大，所以希望能结合多个弱学习器达到近似的效果。因此，它需要关注的两个问题，一是个体学习器如何训练得到，二是如何将个体学习器组合。对这个两个问题的不同解答将集成学习分为以下三种模式：

1. 装袋(Bagging)：个体学习器不存在强相互依赖关系，可同时生成的并行化方法，并行训练多个分类器。对于分类问题，可由模型间相互独立共同投票出结果；对于回归问题，可计算模型的均值作为结果。经典算法如随机森林等。
2. 提升(Boosting)：个体学习器存在强相互依赖关系，必须串行生成序列化方法，通过加法模型将弱分类器线性组合。从弱学习器开始加强，通过加权来进行训练，共同逼近正确答案。经典算法如AdaBoost、XGBoost等。
3. 堆叠(Stacking)：聚合多个分类或回归模型，在多个模型的基础上放置一个更高层的模型，将底层模型的输出作为它的输入，由它给出预测结果。可堆叠各种分类器，经典算法如KNN、SVM等。

图1 集成算法的分类

在AdaBoost之后还出现了许多改进和变体，如Real AdaBoost、SAMME、SAMME.R等，以进一步提高AdaBoost的性能和稳定性，这些变体根据不同的问题和需求进行了调整和优化。还出现了GBDT、XGboost、LightGBM等Boosting方法，应用领域更加广泛，在提高运算速度、处理类别型特征方面各有千秋。不像AdaBoost主要关注分类问题，GBDT（梯度提升决策树）算法主要关注回归问题，它通过计算损失函数的负梯度值（一阶导数）来定位模型的不足，采用决策树作为基学习器，并通过迭代地选择一个指向负梯度方向的函数来优化目标函数。XGBoost（极端梯度提升）算法既可用于分类问题，也可用于回归问题。它加入了衡量模型复杂度的正则项防止模型过拟合，通过利用损失函数的二阶泰勒展开，同时考虑一阶导数和二阶导数信息来优化目标函数。在实现中使用了并行/多核计算，树的生成是并行的，从而提高了训练速度。

不过AdaBoost作为十大经典机器学习算法之一，代表了集成学习领域的一个重要里程碑。它的成功激发了更多关于集成学习和弱学习器的研究，同时也为解决实际问题提供了一个强大的工具。虽然现在有许多其他集成学习算法，但AdaBoost仍然是一个备受尊重的经典方法。

1.3 算法简介

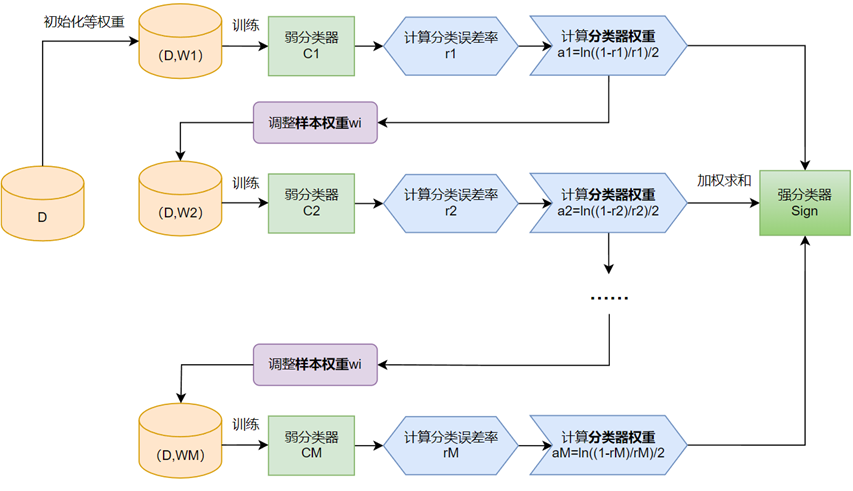
AdaBoost的核心思想是通过加权迭代，不断调整数据样本的权重，使前一轮的错误分类样本在下一轮的训练中得到更多的关注，从而提高分类器性能。其基本步骤是通过动态调整样本的权重来训练一系列弱学习器（通常是简单的决策树或其他分类器）。每一轮训练中，AdaBoost通常使用指数损失函数（Exponential Loss），关注之前分类错误的样本，提高它们的权重，旨在最小化错误分类的样本权重之和，以便下一轮的学习器能够更好地处理它们。最终，AdaBoost使用加权投票策略，将每个弱学习器的预测结果根据其性能被赋予一个权重，最终通过求和的方式得到集成模型的预测结果。多个弱学习器的结果进行加权组合，得到一个强大的集成模型。

AdaBoost的优点是精度比较高，可与各种弱学习器结合使用，例如决策树、朴素贝叶斯、SVM等，因此具有很大的灵活性，可以自动选择重要的特征，从而减少了特征工程的工作量，此外，通过Boosting的方式模型的可解释性很强。

但是它也有缺点，对噪声和异常值敏感、计算开销较大、不适用于高维稀疏数据、容易过拟合等。

总的来说，AdaBoost算法是一种适应大数据时代的强大而高效的集成学习算法，为我们在海量数据中提取有价值信息提供了有力的工具，特别适用于分类问题，如人脸检测、文本分类等。然而，我们也应看到，AdaBoost算法仍有许多可以改进和优化的地方，比如在处理噪声数据、大规模数据和高维稀疏数据等方面可能存在一些困难，并且需要进行参数调优以获得最佳性能，这就需要我们继续深入研究和探索。

2 AdaBoost算法原理详述

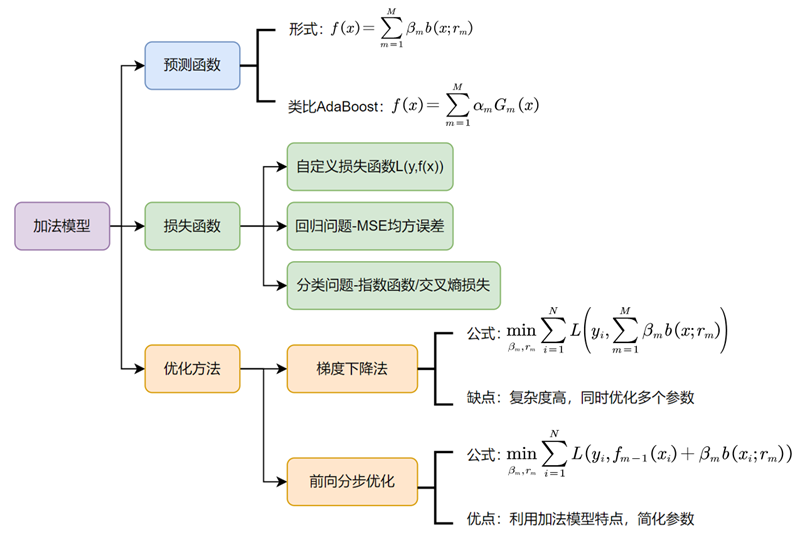
AdaBoost算法使用加法模型，损失函数为指数函数，学习算法使用前向分步算法，主要针对二分类问题。加法模型是指弱学习器的预测会通过加权和的方式结合成一个最终的预测值，这个权重是根据每个弱学习器在训练过程中的表现动态分配的。这种加法模型的思想也体现了一种“三个臭皮匠，顶个诸葛亮”的智慧，即通过组合多个普通的预测模型，可以得到一个更准确的预测模型。

图2 加法模型的特点

2.1 算法流程

1.获取二分类训练数据集：假设有N个样本的训练集，每个样本由实例与标记组成，实例xi∈X，标记yi∈Y={-1,1}，X是实例空间，Y是标记集合。可表示为T={(x1,y1),(x2,y2),…,(xN,yN)}

2.定义基分类器（弱分类器）Gm(x)：可以是阈值分类、逻辑回归、决策树等等，一般保持一致，每个基分类器的训练方法也随之确定，如选择逻辑回归，可以用交叉熵损失函数结合梯度下降进行训练。

3.构建M个基分类器，循环M次。

①初始化或更新当前训练数据的权值分布：赋予训练集中每个样本一个权重，构成权重向量D，第一次将权重向量D初始化相等值1/N。

D1=(w11,…,w1i,…,w1N), w1i=1/N,i=1,2,…,N

若不是第一次根据以下规则确定：提高前一轮“错误分类”的样本的权值，降低前一轮“正确分类”的样本的权值。选择指数损失函数满足该原则。

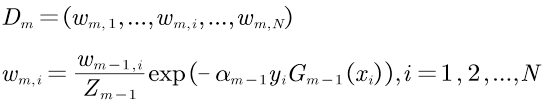
这里，Zm-1是规范化因子，使Dm成为概率分布。

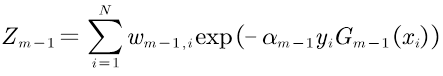
进一步解释wm,i，将其写成如下形式：

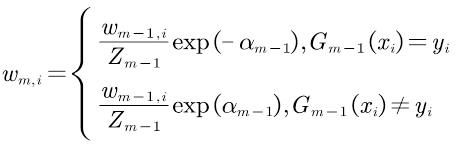
由此可知，被基分类器Gm(x)误分类的样本权重得以扩大，而正确分类的样本权重减小。

②训练当前基分类器Gm(x)，计算分类误差率em，即分类错误样本点的权值累加之和。

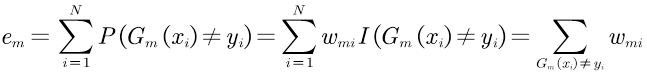
em的范围是[0,0.5]，因为如果训练模型的分类误差率大于0.5可以翻转条件使误差率变为1-em<0.5。

③计算当前基分类器的权值αm：根据加权多数表决，应该加大分类误差率小的弱分类器的权值，使其在表决中起较大作用；减小分类误差率大的弱分类器的权值，使其在表决中起较小作用。即αm和em是负相关，如下图仅考虑0≤em≤0.5部分，计算式为

图3 分类器的权值与误差率的曲线

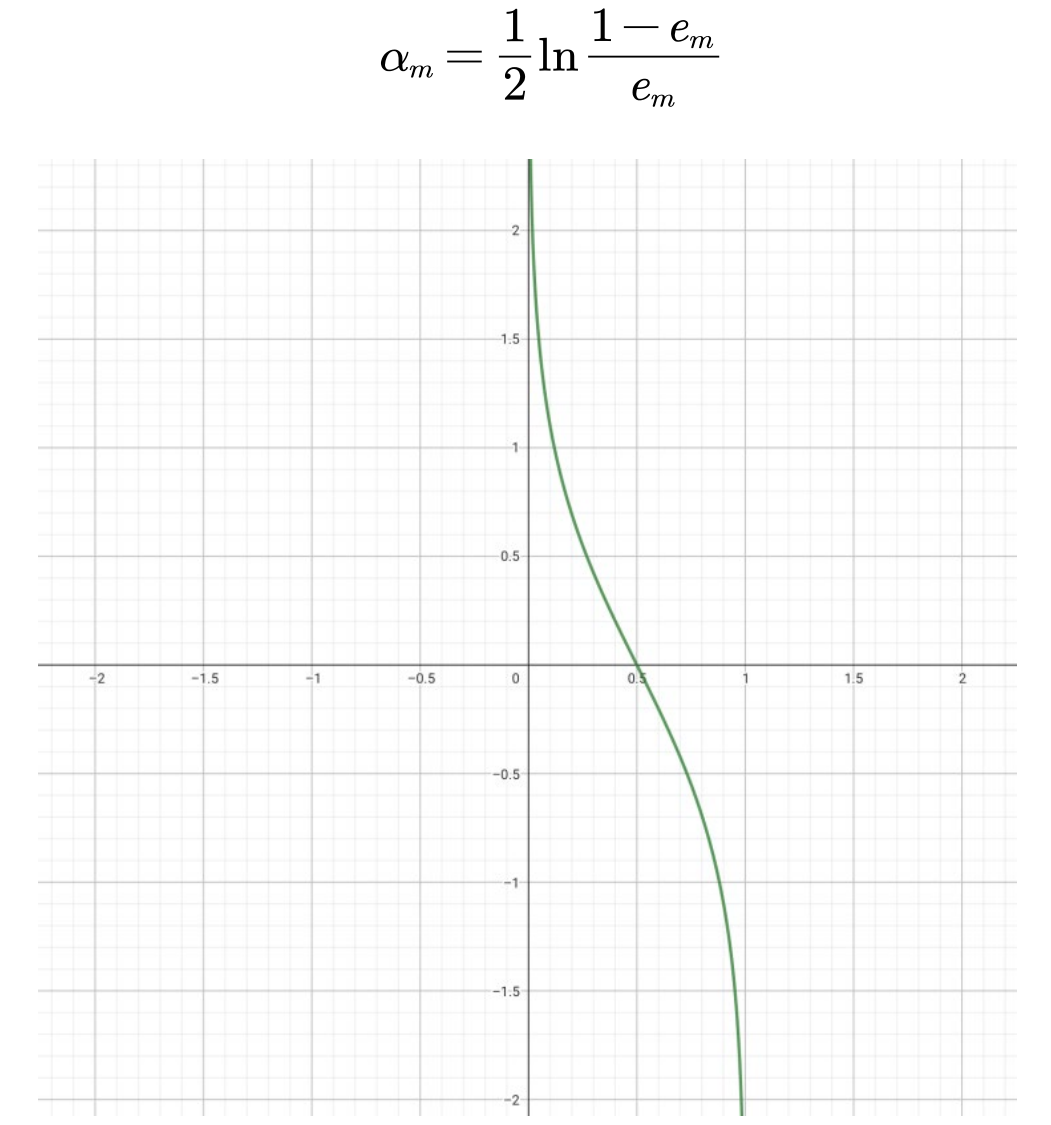
④将αmGm(x)更新到加法模型f(x)中

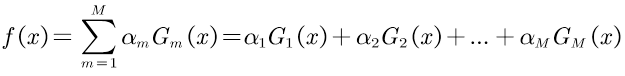
⑤判断是否满足循环退出条件，判断分类器个数是否达到M，或总分类器误差率是否低于设定的精度。

4.最终分类器：f(x)大于0时为1，小于0时为-1,G(x)=sign[f(x)]

图4 AdaBoost算法流程

2.2 损失函数

对于分类问题，可以选择指数损失函数或者交叉熵损失函数，针对二分类问题，且标记值为{-1,1},选择指数损失函数，因为交叉熵损失函数是在标记值为{0,1}时建立的。基本表达式为L(y,f(x))=exp[-yf(x)]

当分类正确时，f(x)与y同号，L(y,f(x))≤1；当分类错误时，f(x)与y异号，L(y,f(x))≥1。故可将损失函数视为训练数据的权值。

单个样本的损失函数：

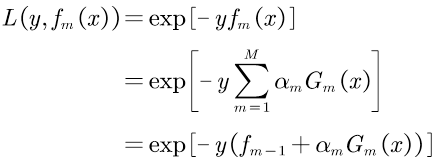
总体的损失函数：

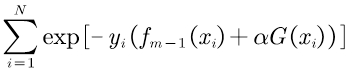
2.3 前向分步优化

类比加法模型的预测函数和AdaBoost可知，AdaBoost属于加法模型，加法模型在优化方法上使用前向分步优化的方法代替传统的梯度下降，充分利用加法模型分步串行的特点，简化了优化参数的计算量。

梯度下降法优化公式：

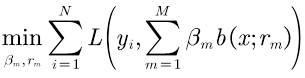
前向分步优化法公式（循环M次）：

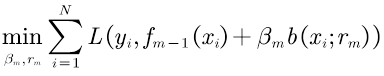
对比公式(13)(14)可见，梯度下降是一次性对所有参数进行优化，假设设计了M个分类器，一次要优化2M个参数，计算量庞大。而前向分步优化用前一步得到的fm-1代替了累加过程，这个值是一个常数，不影响最小值的求解，每次只优化两个参数，可以利用之前的结果并循环M次。

根据2.2中推导了总体损失函数即公式(12)，AdaBoost中需要优化的函数如下：

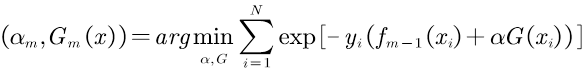
推导过程如下：

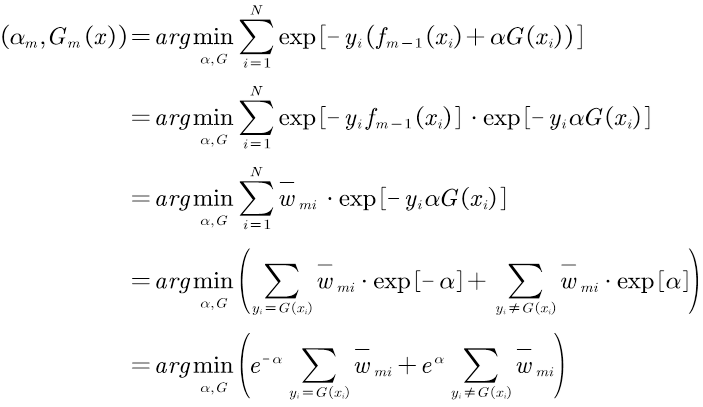
所以原式可以化简为

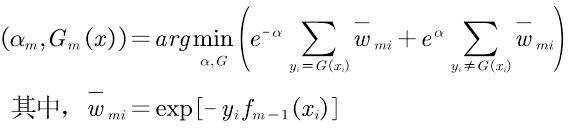
1.优化Gm(x)，使得分类误差率em最小：

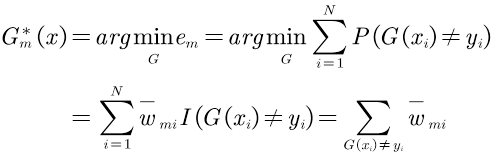
2.优化αm，推导过程如下：

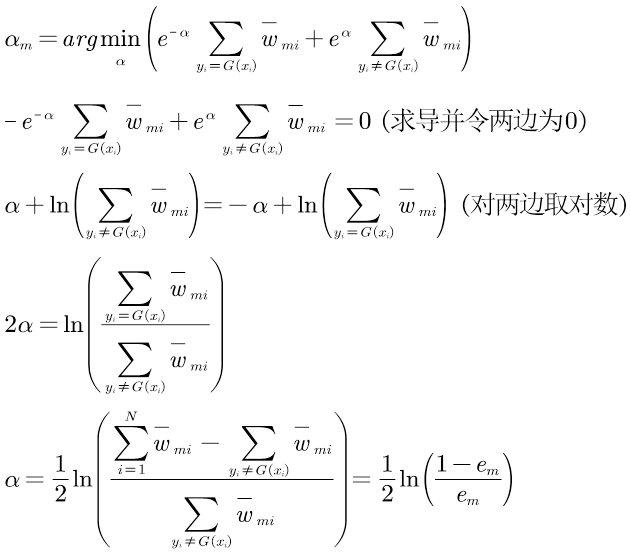
至此，我们推导出了2.1节算法流程中公式的由来，知其然并知其所以然。

3 AdaBoost算法实验

3.1 实验内容

实验目标：将两个类别的点使用AdaBoost模型区分开，并可视化结果，观察AdaBoost的迭代过程。

实验步骤：

1. 创建数据集（使用高斯数据集）。
2. 使用AdaBoostClassifier构建AdaBoost模型。
3. 调用fit方法训练构建好的数据集，创建boosted分类器。
4. 调用predict方法用模型进行预测。
5. 调用score方法评估预测的正确率、模型的精度。
6. 可视化结果，改变n_estimators的值观察AdaBoost迭代过程。

AdaBoostClassifier是scikit-learn（简称 sklearn）提供的关于用AdaBoost做分类的相关模块，可以跳过代码底层，直接使用十分方便。sklearn是一个流行的 Python 库，用于机器学习和数据挖掘任务。它基于 NumPy、SciPy 和 Matplotlib 等数据科学包，提供了许多常用的机器学习算法和功能，如数据集构建、数据预处理、特征选择、降维、分类聚类回归算法、模型评估、神经网络等。

3.2 实现代码

项目已上传至我的github仓库：https://github.com/reasimei/AdaBoost

1. *#-\*- coding: utf-8 -\*-*
2. import numpy as np
3. import matplotlib.pyplot as plt
4. 
5. from sklearn.ensemble import AdaBoostClassifier
6. from sklearn.tree import DecisionTreeClassifier
7. from sklearn.datasets import make_gaussian_quantiles
8. 
9. plt.rcParams['font.sans-serif']=['SimHei'] *#**用来正常显示中文标签*
10. plt.rcParams['axes.unicode_minus']=False *#**用来正常显示负号*
11. 
12. *# 1.**创建数据* *高斯数据集* *cov**方差* *std**标准差* *mean**均值* *默认值**0*
13. x1, y1 = make_gaussian_quantiles(cov=2.,
14. n_samples=200, n_features=2,
15. n_classes=2, random_state=1)
16. x2, y2 = make_gaussian_quantiles(mean=(3, 3), cov=1.5,
17. n_samples=200, n_features=2,
18. n_classes=2, random_state=1)
19. print(x1.shape, y1.shape)
20. print(x2.shape, y2.shape)
21. X = np.concatenate((x1, x2))
22. y = np.concatenate((y1, -y2 + 1))
23. print(X.shape, y.shape)
24. 
25. *# 2.**构建**adaboost**模型*
26. bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1),
27. n_estimators=200)
28. *#* *数据量大的时候* *可以增加内部分类器的树深度* *也可以不限制树深*
29. *# max depth**树深* *数据量大的时候* *一般范围在**10-100**之间*
30. *#* *数据量小的时候* *一般可以设置树深度较小* *或者**n_estimators**较小*
31. 
32. *# n_estimators**迭代次数或者最大弱分类器数：* *200**次*
33. *# base estimators**：**decisiontreeclassifier**选择弱分类器* *默认是**cart**树*
34. *# algorithm**运算方式：**samme* *和* *samme.r* *运算规则* *后者**.r**的是**real**的算法* *以概率调整权重* *迭代速度快更快找到最优的*
35. *#* *需要能计算概率的分类器支持*
36. *# learning rate**：**0~1* *默认为**1* *正则项* *衰减指数* *默认是**1**可以调小* *就是在更新样本权重的时候不要变化太快*
37. *# 3.**为训练集**(X,y)**创建**boosted**分类器*
38. bdt.fit(X, y)
39. *#* *准备画图*
40. plot_step = 0.02
41. x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
42. x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
43. *#* *网格* *背景区域*
44. xx, yy = np.meshgrid(np.arange(x1_min, x1_max, plot_step),
45. np.arange(x2_min, x2_max, plot_step))
46. *# 4.**用模型进行预测*
47. Z = bdt.predict(np.c_[xx.ravel(), yy.ravel()])
48. *#* *设置维度*
49. Z = Z.reshape(xx.shape)
50. *# 5.**可视化结果* *画图*
51. plot_colors = "br"
52. class_names = "AB"
53. plt.figure(figsize=(10, 5), facecolor='w')
54. plt.subplot(121)
55. *#* *画第一个子图的* *分类区域*
56. plt.pcolormesh(xx, yy, Z, shading='auto', cmap=plt.cm.Paired)
57. for i, n, c in zip(range(2), class_names, plot_colors):
58. idx = np.where(y == i)
59. *#* *散点图*
60. plt.scatter(X[idx, 0], X[idx, 1], c=c, cmap=plt.cm.Paired, label=u"类别%s" % n)
61. plt.xlim(x1_min, x1_max)
62. plt.ylim(x2_min, x2_max)
63. plt.legend(loc='upper right')
64. plt.xlabel('x1')
65. plt.ylabel('x2')
66. plt.title(u'AdaBoost算法分类，正确率为： %.2f%%' % (bdt.score(X, y) * 100))
67. 
68. *#* *获取决策函数的数值*
69. *#* *决策函数* *最终的* *200**个弱学习器融合之后的* *计算所有样本的预测值*
70. twoclass_output = bdt.decision_function(X)
71. print('获取决策函数的数值：', twoclass_output)
72. print('获取决策函数的数值长度：', len(twoclass_output))
73. *#* *获取范围*
74. plot_range = (twoclass_output.min(), twoclass_output.max())
75. 
76. plt.subplot(122)
77. for i, n, c in zip(range(2), class_names, plot_colors):
78. *#* *直方图*
79. plt.hist(twoclass_output[y == i],
80. bins=20,
81. range=plot_range,
82. facecolor=c,
83. label=u'类别 %s' % n,
84. alpha=.5)
85. x1, x2, y1, y2 = plt.axis()
86. plt.axis((x1, x2, y1, y2 * 1.2))
87. plt.legend(loc='upper right')
88. plt.ylabel(u'样本数')
89. plt.xlabel(u'决策函数值')
90. plt.title(u'AdaBoost的决策值')
91. plt.tight_layout()
92. plt.subplots_adjust(wspace=0.35)
93. plt.show()

3.3 实验结果

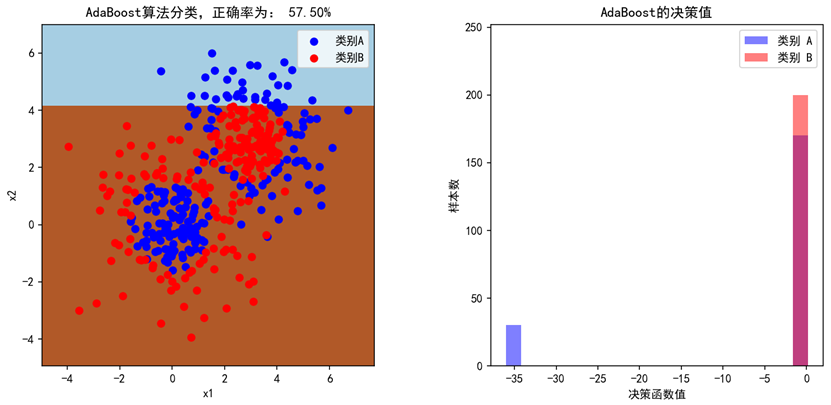
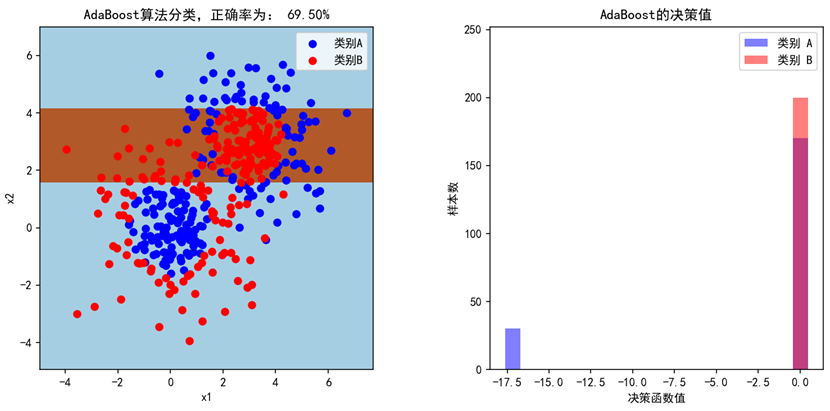
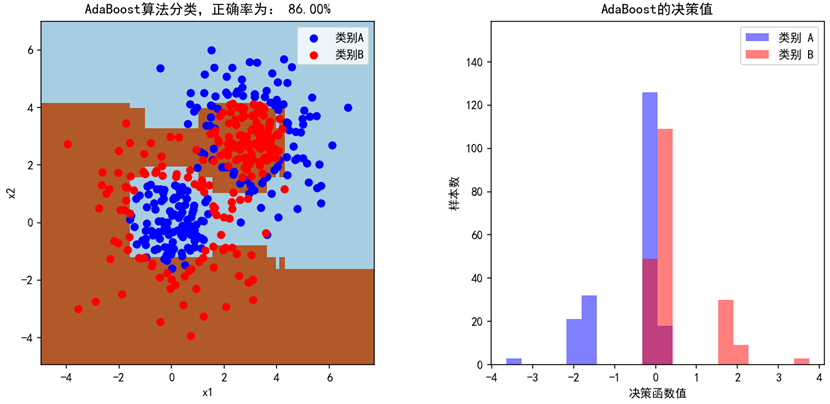
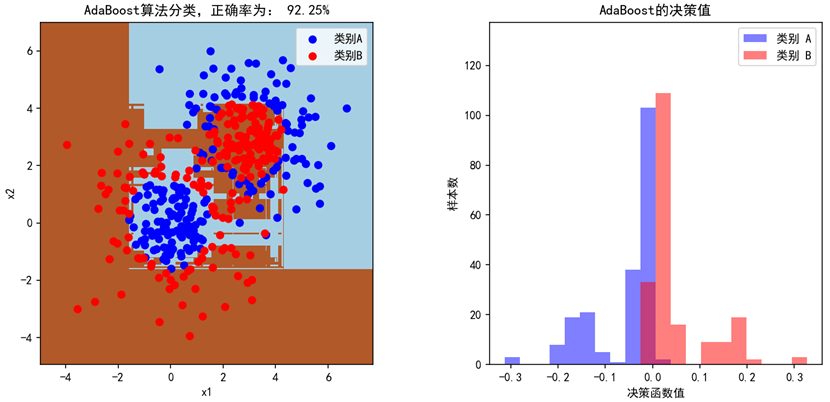
当设置弱学习器的数量为200个时（n_estimators=200），模型的准确率为92.25%，基本能将类别A和类别B的点区分开来。左图是两种点的散点图，模型的预测填充为蓝色和棕色的背景，右图是AdaBoost最终训练出的强学习器对两种分类的决策值。分别设置n_estimators=1,2,20,200,可观察出AdaBoost的迭代过程，第一轮弱学习器准确率只有57.5%，只是简单的画了一条线，接着，随着弱学习器个数增多，分割的次数变多，正确率不断提高。

图5 1个弱学习器实验结果

图6 2个弱学习器实验结果

图7 20个弱学习器实验结果

图8 200个弱学习器实验结果

参考文献

[1] Zhang, Y., Zhang, H., & Long, S. (2018). A Novel Approach to Image Classification Based on AdaBoost. In 2018 IEEE International Conference on Computer Science and Computational Technology (CSCT) (pp. 1-5). IEEE.

[2] 李航. 统计学习方法[M]. Qing hua da xue chu ban she, 2019.

[3] Chen, X., Zhou, Y., & Chen, Y. (2019). Weak Classifier Ensemble for Face Detection Based on AdaBoost. In 2019 IEEE International Conference on Image Processing (ICIP) (pp. 1516-1520). IEEE.

[4] Y. Zhang et al., “Research and Application of AdaBoost Algorithm Based on SVM,” 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 2019, pp. 662-666, doi: 10.1109/ITAIC.2019.8785556.

[5] F. Wang, Z. Li, F. He, R. Wang, W. Yu and F. Nie, “Feature Learning Viewpoint of Adaboost and a New Algorithm,” in IEEE Access, vol. 7, pp. 149890-149899, 2019, doi: 10.1109/ACCESS.2019.2947359.

[6] Wang, Y., Li, J., & Liu, Y. (2018). AdaBoost: An Ensemble Learning Algorithm for Weak Classifier. In 2018 IEEE International Conference on Pattern Recognition and Machine Intelligence (PAMI) (pp. 23-28). IEEE.

[7] Liu, H., Gao, J., & Zhang, L. (2018). AdaBoost for Imbalanced Data Sets: A Survey. In 2018 IEEE International Conference on Data Science and Advanced Analytics (DSAA) (pp. 55-64). IEEE.

[8] CHEN Ganghua, LIANG Shasha, WANG Jun, DI Shuhua, ZHUGE Yueying, LIU Youji. Fluid identification in glutenites with the machine learning AdaBoost.M2 algorithm. Oil Geophysical Prospecting, 2019, 54(6): 1357-1362. DOI: 10.13810/j.cnki.issn.1000-7210.2019.06.020.

[9] 梁云, 门昌骞, 王文剑. 基于模型决策树的 AdaBoost 算法[J]. 《 山东大学学报 (理学版)》, 2023, 58(1): 67-75.

[10] Huang X, Li Z, Jin Y, et al. Fair-AdaBoost: Extending AdaBoost method to achieve fair classification[J]. Expert Systems with Applications, 2022, 202: 117240.

[11] 于玲, 吴铁军. 集成学习: Boosting 算法综述[J]. 模式识别与人工智能, 2004, 17(1): 52-59.